练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）＝Asin（ωx+）（A＞0，ω＞0）的最小正周期为3π，则（　　）

    A. 函数f（x）的一个零点为

    B. 函数f（x）的图象关于直线x＝对称

    C. 函数f（x）图象上的所有点向左平移个单位长度后，所得的图象关于y轴对称

    D. 函数f（x）在（0，）上单调递增

    【答案】C

    【解析】

    利用三角函数的周期性求得的值，可得函数的解析式，再利用三角函数的图象和性质，逐一检验选项中的结论是否正确，即可得出结论.

    函数的最小正周期为，

    函数 ，

    令，故不是函数的一个零点，故错误；

    令不是最值，故不是函数的图象的对称轴，故错误；

    把函数图象上的所有点向左平移个单位长度后，

    可得的图象，

    这是一个偶函数，故所得的图象关于轴对称，故正确；

    在上，，函数不是单调函数,

    故错误，故选C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某校从参加高三模拟考试的学生中随机抽取60名学生，将其数学成绩（均为整数）分成六组[90，100），[100，110），…，[140，150]后得到如下部分频率分布直方图，观察图形的信息，回答下列问题：

    （1）求分数在[120，130）内的频率；

    （2）估计本次考试的中位数；

    （3）用分层抽样的方法在分数段为[110，130）的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任取2人，求至多有1人在分数段[120，130）内的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列叙述中正确的是(　 　)

    A. 若，则“”的充要条件是“”

    B. 函数的最大值是

    C. 命题“”的否定是“”

    D. 是一条直线，是两个不同的平面，若则

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了调查高一学生在分班选科时是否选择物理科目与性别的关系，随机调查100名高一学生，得到列联表如下：由此得出的正确结论是( )

    选择物理

    不选择物理

    总计

    男

    35

    20

    55

    女

    15

    30

    45

    总计

    50

    50

    100

    附：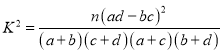

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    A.在犯错误的概率不超过0.01的前提下，认为“选择物理与性别有关”

    B.在犯错误的概率不超过0.01的前提下，认为“选择物理与性别无关”

    C.有的把握认为“选择物理与性别有关”

    D.有的把握认为“选择物理与性别无关”

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为调查某地区老年人是否需要志愿者提供帮助，用简单随机抽样的方法从该地区调查了500位老年人，结果如下：

    性别

    是否需要志愿者

    男

    女

    需要

    40

    30

    不需要

    160

    270

    附：的观测值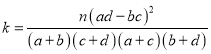

    0.05

    0.01

    0.001

    3.841

    6.635

    10.828

    （1）估计该地区老年人中，需要志愿者提供帮助的老年人的比例；

    （2）在犯错误的概率不超过0.01的前提下是否可认为该地区的老年人是否需要志愿者提供帮助与性别有关？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某单位有员工1000名，平均每人每年创造利润10万元，为了增加企业竞争力，决定优化产业结构，调整出x（x∈N*）名员工从事第三产业，调整后他们平均每人每年创造利润为10（a﹣0.8x%）万元（a＞0），剩下的员工平均每人每年创造的利润可以提高0.4x%．

    （1）若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润，则最多调整出多少名员工从事第三产业？

    （2）若要保证剩余员工创造的年总利润不低于原来1000名员工创遣的年总利润条件下，若要求调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润，则a的取值范围是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）＝sin（）的图象与函数g（x）的图象关于x＝1对称，则函数g（x）在（﹣6，﹣4）上（　　）

    A. 单调递增 B. 单调递减 C. 先增后减 D. 先减后增

    查看答案和解析>>

    科目：高中数学 来源： 题型：

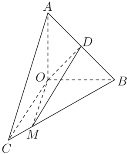
    【题目】如图，在直角△中，，△通过△以直线为轴顺时针旋转120°得到（），点为线段上一点，且.

    （1）求证：，并证明：平面；

    （2）分别以、、为、、轴建立空间直角坐标系，求异面直线与所成角的大小（用反余弦运算表示）；

    （3）若，求锐二面角的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在数学上，常用符号来表示算式，如记=，其中，.

    （1）若，，，…，成等差数列，且，求证：；

    （2）若，，记，且不等式恒成立，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案