
| A. | “b2=ac”是“a,b,c成等比数列”的充要条件 | |
| B. | “?x∈R,x2>0”的否定是“?x0∈R,x02>0” | |
| C. | “若a=-4,则函数f(x)=ax2+4x-1只有唯一一个零点”的逆命题为真命题 | |
| D. | “函数f(x)=lnx2与函数g(x)=$\left\{\begin{array}{l}{2lnx,x>0}\\{2ln(-x),x<0}\end{array}\right.$的图象相同” |
分析 举例说明A错误;直接写出全称命题的否定判断B;举例说明C错误;写出分段函数说明D正确.
解答 解:A错误,如a=0,b=0,c=1满足b2=ac,但a,b,c不成等比数列;
B错误,“?x∈R,x2>0”的否定是“?x0∈R,x02≤0”
C错误,“若a=-4,则函数f(x)=ax2+4x-1只有唯一一个零点”的逆命题是:“若函数f(x)=ax2+4x-1只有唯一一个零点,则a=-4”,为假命题,
比如a=0,f(x)=0的根是$\frac{1}{4}$;
D正确,函数f(x)=lnx2是分段函数,分x>0和x<0分段可得函数g(x)=$\left\{\begin{array}{l}{2lnx,x>0}\\{2ln(-x),x<0}\end{array}\right.$.
故选:D.
点评 本题考查命题的真假判断与应用,考查了等比数列的判定,考查命题的否定,训练了函数零点的求法,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设函数f(x)=log2(x-a)(a∈R).
设函数f(x)=log2(x-a)(a∈R).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
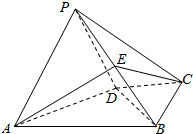 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,∠ABC=90°,AB=2,AD=$\sqrt{2}$,PA=PD=CD=CB=1,E总是线段PB上的动点.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,∠ABC=90°,AB=2,AD=$\sqrt{2}$,PA=PD=CD=CB=1,E总是线段PB上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x=-$\frac{π}{4}$ | B. | x=$\frac{π}{4}$ | C. | x=$\frac{π}{2}$ | D. | x=π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2m/s | B. | 0m/s | C. | 4m/s | D. | -4m/s |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com