
分析 化简函数f(x),分a≤-1时,-1<a<1时,a≥1时,利用函数的单调性即可求出答案.
解答 解:f(x)=cos2x+2asinx+3a-1=1-sin2x+2asinx+3a-1=-sin2x+2asinx+3a=-(sinx-a)2+3a+a2,sinx∈[-1,1],
令sinx=t,t∈[-1,1],
∴f(t)=-(t-a)2+3a+a2对称轴为t=a,
当a≤-1时,函数f(t)在[-1,1]上是减函数,∴f(x)max=f(-1)=a-1=4,解得a=5,舍去
当-1<a<1时,函数f(t)在[-1,a]上为增函数,在(a,1)上为减函数,∴f(x)max=f(a)=3a+a2=4,解得a=1或a=-4,舍去,
当a≥1时,函数f(t)在[-1,1]上是增函数,∴f(x)max=f(1)=5a-1=4,解得a=1,
综上所述,存在实数a=1,使函数f(x)=cos2x+2asinx+3a-1在闭区间上的最大值为 4
点评 本题考查了二倍角公式以及二次函数的性质与应用问题,也考查了分类讨论的数学思想,属于中档题


 优学名师名题系列答案
优学名师名题系列答案科目:高中数学 来源: 题型:选择题
| A. | 空间四边形 | B. | 任意的四边形 | C. | 梯形 | D. | 平行四边形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
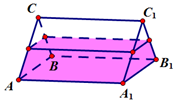 如图,一个直三棱柱形容器中盛有水,且侧棱AA1=8.若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的中点,当底面ABC水平放置时,液面高为( )
如图,一个直三棱柱形容器中盛有水,且侧棱AA1=8.若侧面AA1B1B水平放置时,液面恰好过AC,BC,A1C1,B1C1的中点,当底面ABC水平放置时,液面高为( )| A. | 7 | B. | 6 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分条件又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{4}$) | B. | [$\frac{1}{4}$,1) | C. | ($\frac{1}{16}$,1) | D. | [$\frac{1}{16}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $?x∈R,\root{3}{x}+1>0$ | |
| B. | 小概率事件就是不可能发生的事件,大概率事件就是必然要发生的事件 | |
| C. | p∨q为真命题,则命题p与q均为真命题 | |
| D. | 命题“$?{x_0}∈R,{x_0}^2-{x_0}>0$的命题的否定是“?x∈R,x2-x≤0” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a1+a8=a4+a5 | B. | a1+a8<a4+a5 | ||
| C. | a1+a8>a4+a5 | D. | a1+a8与a4+a5大小关系不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com