
【题目】曲线![]() 上动点
上动点![]() 到定点
到定点![]() 与定直线
与定直线![]() 的距离之比为常数
的距离之比为常数![]() ;
;
(1)求曲线![]() 的轨迹方程;
的轨迹方程;
(2)设圆心为![]() 的圆
的圆![]()
![]() 与曲线
与曲线![]() 交于点
交于点![]() 与点
与点![]() ,求
,求![]() 的最小值,并求此时圆
的最小值,并求此时圆![]() 的方程;
的方程;
科目:高中数学 来源: 题型:
【题目】2014年7月18日15时,超强台风“威马逊”登陆海南省.据统计,本次台风造成全省直接经济损失119.52亿元.适逢暑假,小明调查住在自己小区的50户居民由于台风造成的经济损失,作出如下频率分布直方图:
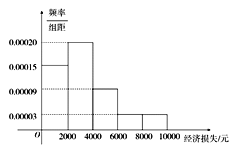
经济损失 4000元以下 | 经济损失 4000元以上 | 合计 | |
捐款超过500元 | 30 | ||
捐款低于500元 | 6 | ||
合计 |
(1)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如上表,在表格空白处填写正确数字,并说明是否有![]() 以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
(2)台风造成了小区多户居民门窗损坏,若小区所有居民的门窗均由李师傅和张师傅两人进行维修,李师傅每天早上在7:00到8:00之间的任意时刻来到小区,张师傅每天早上在7:30到8:30分之间的任意时刻来到小区,求连续3天内,李师傅比张师傅早到小区的天数的数学期望.
附:临界值表
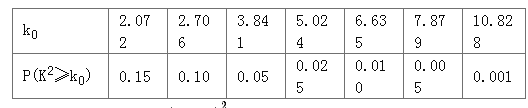
参考公式: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业在“精准扶贫”行动中,决定帮助一贫困山区将水果运出销售.现有8辆甲型车和4辆乙型车,甲型车每次最多能运6吨且每天能运4次,乙型车每次最多能运10吨且每天能运3次,甲型车每天费用320元,乙型车每天费用504元.若需要一天内把180吨水果运输到火车站,则通过合理调配车辆运送这批水果的费用最少为______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设曲线![]() 上一点
上一点![]() 到焦点的距离为3.
到焦点的距离为3.
(1)求曲线C方程;
(2)设P,Q为曲线C上不同于原点O的任意两点,且满足以线段PQ为直径的圆过原点O,试问直线PQ是否恒过定点?若恒过定点,求出定点坐标;若不恒过定点,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足:对于任意正数
满足:对于任意正数![]() ,都有
,都有![]() ,且
,且![]() ,则称函数
,则称函数![]() 为“L函数”.
为“L函数”.
(1)试判断函数![]() 与
与![]() 是否是“L函数”;
是否是“L函数”;
(2)若函数![]() 为“L函数”,求实数a的取值范围;
为“L函数”,求实数a的取值范围;
(3)若函数![]() 为“L函数”,且
为“L函数”,且![]() ,求证:对任意
,求证:对任意![]() ,都有
,都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
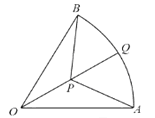
【题目】如图,三个校区分别位于扇形OAB的三个顶点上,点Q是弧AB的中点,现欲在线段OQ上找一处开挖工作坑P(不与点O,Q重合),为小区铺设三条地下电缆管线PO,PA,PB,已知OA=2千米,∠AOB=![]() ,记∠APQ=θrad,地下电缆管线的总长度为y千米.
,记∠APQ=θrad,地下电缆管线的总长度为y千米.
(1)将y表示成θ的函数,并写出θ的范围;
(2)请确定工作坑P的位置,使地下电缆管线的总长度最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】纪念币是一个国家为纪念国际或本国的政治、历史,文化等方面的重大事件、杰出人物、名胜古迹、珍稀动植物、体育赛事等而发行的法定货币.我国在1984年首次发行纪念币,目前已发行了115套纪念币,这些纪念币深受邮币爱好者的喜爱与收藏.2019年发行的第115套纪念币“双遗产之泰山币”是目前为止发行的第一套异形币,因为这套纪念币的多种特质,更加受到爱好者追捧.某机构为调查我国公民对纪念币的喜爱态度,随机选了某城市某小区的50位居民调查,调查结果统计如下:
喜爱 | 不喜爱 | 合计 | |
年龄不大于40岁 | 24 | ||
年龄大于40岁 | 20 | ||
合计 | 22 | 50 |
(1)根据已有数据,把表格数据填写完整,判断能否在犯错误的概率不超过![]() 的前提下认为不同年龄与纪念币的喜爱无关?
的前提下认为不同年龄与纪念币的喜爱无关?
(2)已知在被调查的年龄不大于40岁的喜爱者中有5名男性,其中3位是学生,现从这5名男性中随机抽取2人,求至多有1位学生的概率.
附: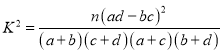 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com