
分析 (a+1)2+(b+1)2的几何意义是点(-1,-1)和直线a+b=1上的点的距离的平方,作出直线a+b=1,由点到直线的距离公式计算即可得到最小值.
解答 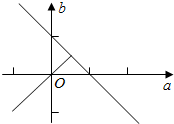 解:(a+1)2+(b+1)2的几何意义是:
解:(a+1)2+(b+1)2的几何意义是:
点(-1,-1)和直线a+b=1上的点的距离的平方,
作出直线a+b=1,可得点(-1,-1)到直线的距离的平方,即为最小值.
由d=$\frac{|-1-1-1|}{\sqrt{2}}$=$\frac{3\sqrt{2}}{2}$,
即有最小值为$\frac{9}{2}$.
故答案为:$\frac{9}{2}$.
点评 本题考查直线方程的运用,考查最小值的求法,注意运用几何意义,结合图形解决是解题的关键.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|x≥-$\frac{3}{2}$} | B. | {x|x≥-$\frac{3}{2}$且x≠0} | C. | {x|x≤$\frac{3}{2}$} | D. | {x|x≤$\frac{3}{2}$且x≠0} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A<B<C | B. | B<C<A | C. | A<C<B | D. | B<A<C |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>0是1a<1b的充要条件 | |
| B. | 若a+b+c=0,则a>b>c是ac<0的充分而不必要条件 | |
| C. | ac2>bc2是a>b的必要而不充分条件 | |
| D. | a>b且c>d是a-c>b-d的必要不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5$\sqrt{2}$ | B. | 8 | C. | 6$\sqrt{3}$ | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com