
【题目】设计一个随机试验,使一个事件的概率与某个未知数有关,然后通过重复试验,以频率估计概率,即可求得未知数的近似解,这种随机试验在数学上称为随机模拟法,也称为蒙特卡洛法。比如要计算一个正方形内部不规则图形的面积,就可以利用撒豆子,计算出落在不规则图形内部和正方形内部的豆子数比近似等于不规则图形面积与正方形面积比,从而近似求出不规则图形的面积.
统计学上还有一个非常著名的蒲丰投针实验:平面上间隔![]() 的平行线,向平行线间的平面上任意投掷一枚长为
的平行线,向平行线间的平面上任意投掷一枚长为![]() 的针
的针![]() ,通过多次实验可以近似求出针与任一平行线(以
,通过多次实验可以近似求出针与任一平行线(以![]() 为例)相交(当针的中点在平行线外不算相交)的概率.以
为例)相交(当针的中点在平行线外不算相交)的概率.以![]() 表示针的中点与最近一条平行线
表示针的中点与最近一条平行线![]() 的距离,又以
的距离,又以![]() 表示
表示![]() 与
与![]() 所成夹角,如图甲,易知满足条件:
所成夹角,如图甲,易知满足条件:![]() ,
,![]() .
.
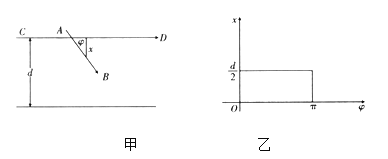
由这两式可以确定平面上的一个矩形![]() ,如图乙,在图甲中,当
,如图乙,在图甲中,当![]() 满足___________(
满足___________(![]() 与
与![]() ,
,![]() 之间的关系)时,针与平行线相交(记为事件
之间的关系)时,针与平行线相交(记为事件![]() ).可用从实验中获得的频率去近似
).可用从实验中获得的频率去近似![]() ,即投针
,即投针![]() 次,其中相交的次数为
次,其中相交的次数为![]() ,则
,则![]() ,历史上有一个数学家亲自做了这实验,他投掷的次数是5000,相交的次数为2550次,
,历史上有一个数学家亲自做了这实验,他投掷的次数是5000,相交的次数为2550次,![]() ,
,![]() ,依据这个实验求圆周率
,依据这个实验求圆周率![]() 的近似值_________.(精确到3位小数)
的近似值_________.(精确到3位小数)
科目:高中数学 来源: 题型:
【题目】已知![]() ,其中
,其中![]() .
.
(1)若![]() ,写出
,写出![]() 的单调区间:
的单调区间:
(2)若函数![]() 恰有三个不同的零点,且这些零点之和为-2,求a、b的值;
恰有三个不同的零点,且这些零点之和为-2,求a、b的值;
(3)若函数![]() 在
在![]() 上有四个不同零点
上有四个不同零点![]() ,求
,求![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]()
(l)设![]() 为参数,若
为参数,若![]() ,求直线
,求直线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 设
设![]() ,且
,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是函数![]() 在区间
在区间![]() 上的图象,为了得到这个函数的图象,只需将
上的图象,为了得到这个函数的图象,只需将![]() 的图象上的所有的点( )
的图象上的所有的点( )
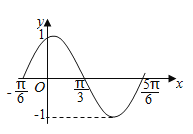
![]()
A.向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
B.向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
C.向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的
个长度单位,再把所得各点的横坐标变为原来的![]() ,纵坐标不变
,纵坐标不变
D.向左平移![]() 个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义![]() ,已知函数
,已知函数![]() 、
、![]() 定义域都是
定义域都是![]() ,给出下列命题:
,给出下列命题:
(1)若![]() 、
、![]() 都是奇函数,则函数
都是奇函数,则函数![]() 为奇函数;
为奇函数;
(2)若![]() 、
、![]() 都是减函数,则函数
都是减函数,则函数![]() 为减函数;
为减函数;
(3)若![]() ,
,![]() ,则
,则![]() ;
;
(4)若![]() 、
、![]() 都是周期函数,则函数
都是周期函数,则函数![]() 是周期函数.
是周期函数.
其中正确命题的个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】焦点在x轴上的椭圆C:![]() 经过点
经过点![]() ,椭圆C的离心率为
,椭圆C的离心率为![]() .
.![]() ,
,![]() 是椭圆的左、右焦点,P为椭圆上任意点.
是椭圆的左、右焦点,P为椭圆上任意点.
(1)求椭圆的标准方程;
(2)若点M为![]() 的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数
的中点(O为坐标原点),过M且平行于OP的直线l交椭圆C于A,B两点,是否存在实数![]() ,使得
,使得![]() ;若存在,请求出
;若存在,请求出![]() 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,某小区中有条长为50米,宽为6.5米的道路ABCD,在路的一侧可以停放汽车,已知小型汽车的停车位是一个2.5米宽,5米长的矩形,如GHPQ,这样该段道路可以划岀10个车位,随着小区居民汽车拥有量的增加,停车难成为普遍现象.经过各方协商,小区物业拟压缩绿化,拓宽道路,改变车位方向增加停车位,如图2,改建后的通行宽度保持不变,即G到AD的距离不变.
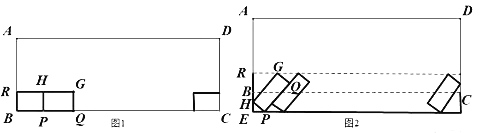
(1)绿化被压缩的宽度BE与停车位的角度∠HPE有关,记![]() 为停车方便,要求
为停车方便,要求![]() ,写出
,写出![]() 关于
关于![]() 的函数表达式
的函数表达式![]() ;
;
(2)沿用(1)的条件和记号,实际施工时,BE=3米,问改造后的停车位增加了多少个?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 满足
满足![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,写出
,写出![]() 所有可能的值;
所有可能的值;
(2)若数列![]() 是递增数列,且
是递增数列,且![]() 、
、![]() 、
、![]() 成等差数列,求p的值;
成等差数列,求p的值;
(3)若![]() ,且
,且![]() 是递增数列,
是递增数列,![]() 是递减数列,求数列
是递减数列,求数列![]() 的通项公式.
的通项公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com