练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    P是双曲线数学公式-数学公式=1（a＞0，b＞0）右支上一点，F1、F2分别是左、右焦点，且焦距为2c，则△PF1F2的内切圆圆心的横坐标为________．

    a
    分析：根据题意，利用切线长定理，再利用双曲线的定义，把|PF1|-|PF2|=2a，转化为|HF1|-|HF2|=2a，从而求得点H的横坐标．
    解答：如图所示：F1（-c，0）、F2（c，0），设内切圆与x轴的切点是点H，PF1、PF2分 与内切圆的切点分别为M、N，
    ∵由双曲线的定义可得|PF1|-|PF2|=2a，由圆的切线长定理知，|PM|=|PN|，故|MF1|-|NF2 |=2a，
    即|HF1|-|HF2|=2a，设内切圆的圆心横坐标为x，则点H的横坐标为x，
    故 （x+c）-（c-x）=2a，∴x=a．
    故答案为：a．

    点评：本题考查双曲线的定义、切线长定理，体现了转化的数学思想以及数形结合的数学思想．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

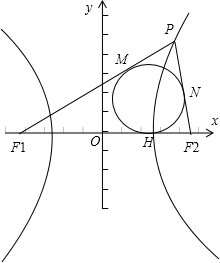
    科目：高中数学 来源：2010-2011学年浙江省温州市十校联考高二（下）期末数学试卷（文科）（解析版） 题型：选择题

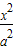    已知点P是双曲线-=1（a＞0，b＞0）右支上一点，F1，F2分别是双曲线的左、右焦点，I为△PF1F2的内心（内心--角平分线交点且满足到三角形各边距离相等），若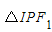 S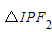=S+S成立，则双曲线的离心率为（ ）
    A．
    B．
    C．4
    D．2

    查看答案和解析>>

    科目：高中数学 来源：2010年福建省漳州一中高三质量检查数学试卷（理科）（解析版） 题型：填空题

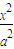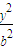    P是双曲线-=1（a＞b＞0）上的点，F1，F2是其焦点，双曲线的离心率是，且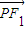•=0，若△F1PF2的面积为9，则a+b=    ．

    查看答案和解析>>

    科目：高中数学 来源：2013年广东省韶关市高考数学二模试卷（理科）（解析版） 题型：填空题

    设点P是双曲线-=1（a＞0，b＞0）与圆x2+y2=a2+b2在第一象限的交点，其中F1，F2分别是双曲线的左、右焦点，若tan∠PF2F1=3，则双曲线的离心率为    ．

    查看答案和解析>>

    科目：高中数学 来源：2010年浙江省高考数学最新押题卷（文科）（解析版） 题型：解答题

    椭圆与双曲线之间有许多类似的性质：
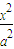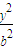    P是椭圆+=1（a＞b＞0）上任一点，焦点F1、F2，∠F1PF2=α，三角形PF1F2面积为b2，类比，P是双曲线-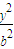=1（a＞0，b＞0）上任一点，焦点F1、F2，∠F1PF2=α，三角形PF1F2面积为    ．

    查看答案和解析>>

    科目：高中数学 来源：广东省高考数学一轮复习：9.3 双曲线的定义与标准方程（解析版） 题型：解答题

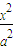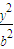    P是双曲线-=1（a＞0，b＞0）右支上一点，F1、F2分别是左、右焦点，且焦距为2c，则△PF1F2的内切圆圆心的横坐标为    ．

    查看答案和解析>>

    同步练习册答案