
 交于不同两点E
交于不同两点E ,F,问是否存在直线l,使得向量
,F,问是否存在直线l,使得向量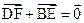 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由. 圆M内,
圆M内, ,且|CM|=R-r,
,且|CM|=R-r,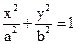 (a>b>0),则a=4,c=2,
(a>b>0),则a=4,c=2,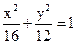 .…5分
.…5分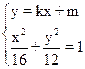 消去y 化简整理得:(3+4k2)x2+8kmx+4m2-48=0,
消去y 化简整理得:(3+4k2)x2+8kmx+4m2-48=0,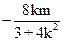 .
. ……7分
……7分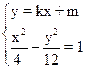 消去y 化简整理得:(3-k2)x2-2kmx-m2-12=0,
消去y 化简整理得:(3-k2)x2-2kmx-m2-12=0, 3+x4=
3+x4=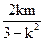 .
.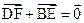 ,∴ (x4-x2 )+ (x3-x1) =0,即x1+x2= x3+x4,
,∴ (x4-x2 )+ (x3-x1) =0,即x1+x2= x3+x4,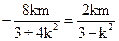 ,∴2km=0或
,∴2km=0或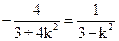 ,
,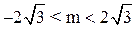 ,
,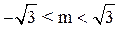 ,∵k∈Z,∴k=-1,0,1.
,∵k∈Z,∴k=-1,0,1.

 名校课堂系列答案
名校课堂系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com