
【题目】如图,在三棱柱ABC-A1B1C1中,B1B=B1A=AB=BC,∠B1BC=90°,D为AC的中点,AB⊥B1D.
(1)求证:平面ABB1A1⊥平面ABC;
(2)在线段CC1(不含端点)上,是否存在点E,使得二面角E-B1D-B的余弦值为-![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
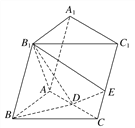
【答案】(1)见解析;(2)在线段CC1上存在点E, ![]()
【解析】试题分析:(1)根据面面垂直的判定定理先证明线面垂直OD⊥平面ABB1A1 然后再证明面面垂直(2)建立空间直角坐标系,求平面的法向量,利用向量法进行求解
解析:(1)证明 取AB的中点O,连接OD,OB1.因为B1B=B1A,所以OB1⊥AB.
又AB⊥B1D,OB1∩B1D=B1,OB1平面B1OD,B1D平面B1OD,
所以AB⊥平面B1OD,
因为OD平面B1OD,所以AB⊥OD.
由已知条件知,BC⊥BB1,
又OD∥BC,所以OD⊥BB1.
因为AB∩BB1=B,AB平面ABB1A1,BB1平面ABB1A1,
所以OD⊥平面ABB1A1.
因为OD平面ABC,所以平面ABB1A1⊥平面ABC.
(2)解 由(1)知OB,OD,OB1两两垂直,所以以O为坐标原点,![]() ,
,![]() ,
,![]() 的方向分别为x轴,y轴,z轴的正方向,|
的方向分别为x轴,y轴,z轴的正方向,|![]() |为单位长度1,建立如图所示的空间直角坐标系,连接B1C.
|为单位长度1,建立如图所示的空间直角坐标系,连接B1C.
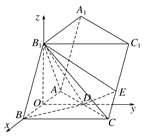
由题设知,B1(0,0,![]() ),B(1,0,0),D(0,1,0),A(-1,0,0),C(1,2,0),C1(0,2,
),B(1,0,0),D(0,1,0),A(-1,0,0),C(1,2,0),C1(0,2,![]() ),
),
∴![]() =(0,1,-
=(0,1,-![]() ),
),![]() =(1,0,-
=(1,0,-![]() ),
),![]() =(-1,0,
=(-1,0,![]() ),
),
![]() =(1,2,-
=(1,2,-![]() ),设
),设![]() =λ
=λ![]() (0<λ<1),
(0<λ<1),
由![]() =
=![]() +
+![]() =(1-λ,2,
=(1-λ,2,![]() (λ-1)),设平面BB1D的法向量为m=(x1,y1,z1),
(λ-1)),设平面BB1D的法向量为m=(x1,y1,z1),
则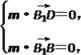 得
得![]()
令z1=1,则x1=y1=![]() ,
,
所以平面BB1D的法向量为m=(![]() ,
,![]() ,1).
,1).
设平面B1DE的法向量为n=(x2,y2,z2),则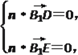
得![]()
令z2=1,则x2=![]() ,y2=
,y2=![]() ,
,
所以平面B1DE的一个法向量n=(![]() ,
,![]() ,1).
,1).
设二面角E-B1D-B的大小为θ,
则cosθ=![]() =
=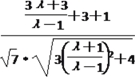 =-
=-![]() .
.
解得λ=![]() .
.
所以在线段CC1上存在点E,使得二面角E-B1D-B的余弦值为-![]() ,此时
,此时![]() =
=![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ),
),![]() .
.
(1)若![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴垂直,求
轴垂直,求![]() 的值;
的值;
(2)若![]() ,试探究函数
,试探究函数![]() 与
与![]() 的图象在其公共点处是否存在公切线.若存在,研究
的图象在其公共点处是否存在公切线.若存在,研究![]() 值的个数;,若不存在,请说明理由.
值的个数;,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() 在点(1,1)处的切线方程为x+y=2.
在点(1,1)处的切线方程为x+y=2.
(1)求a,b的值;
(2)对函数f(x)定义域内的任一个实数x,不等式f(x)-![]() <0恒成立,求实数m的取值范围.
<0恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
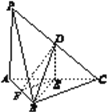
【题目】如图,在三棱锥P-ABC中,D,E,F分别为PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.
求证:(1)直线PA∥平面DEF;
(2)平面BDE⊥平面ABC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学家发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学,给所有同学几何和代数各一题,让各位同学自由选择一道题进行解答.统计情况如下表:(单位:人)
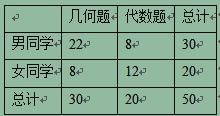
(1)能否据此判断有![]() 的把握认为视觉和空间能力与性别有关?
的把握认为视觉和空间能力与性别有关?
(2)经过多次测试发现:女生甲解答一道几何题所用的时间在5—7分钟,女生乙解答一道几何题所用的时间在6—8分钟,现甲、乙两人独立解答同一道几何题,求乙比甲先解答完的概率;
(3)现从选择几何题的8名女生中任意抽取两人对她们的答题情况进行研究,记甲、乙两名女生被抽到的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表及公式

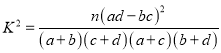
查看答案和解析>>
科目:高中数学 来源: 题型:
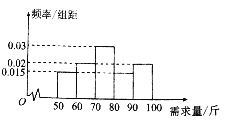
【题目】在某单位的食堂中,食堂每天以10元/斤的价格购进米粉,然后以4.4元/碗的价格出售,每碗内含米粉0.2斤,如果当天卖不完,剩下的米粉以2元/斤的价格卖给养猪场.根据以往统计资料,得到食堂某天米粉需求量的频率分布直方图如图所示,若食堂购进了80斤米粉,以![]() (斤)(其中
(斤)(其中![]() )表示米粉的需求量,
)表示米粉的需求量, ![]() (元)表示利润.
(元)表示利润.
(1)计算当天米粉需求量的平均数,并直接写出需求量的众数和中位数;
(2)估计该天食堂利润不少于760元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年5月14日,第一届“一带一路”国际高峰论坛在北京举行,为了解不同年龄的人对“一带一路”关注程度,某机构随机抽取了年龄在15-75岁之间的100人进行调查, 经统计“青少年”与“中老年”的人数之比为9:11
关注 | 不关注 | 合计 | |
青少年 | 15 | ||
中老年 | |||
合计 | 50 | 50 | 100 |
(1)根据已知条件完成上面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为关注“一带一路”是否和年龄段有关?
的把握认为关注“一带一路”是否和年龄段有关?
(2)现从抽取的青少年中采用分层抽样的办法选取9人进行问卷调查.在这9人中再选取3人进行面对面询问,记选取的3人中关注“一带一路”的人数为X,求X的分布列及数学期望.
附:参考公式 ,其中
,其中![]()
临界值表:
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com