
【题目】已知函数![]() .
.
(1)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,对于任意正实数
时,对于任意正实数![]() ,不等式
,不等式![]() 恒成立,试判断实数
恒成立,试判断实数![]() 的大小关系.
的大小关系.
【答案】(1)![]() 增
增![]() 减;(2)
减;(2)![]()
【解析】
(1)求出导数再讨论a即可判断单调性.(2)设g(x)=f(x)﹣b![]() ,x>0,求导数判断单调性求出极值,转化为g(x)max≤0即可.
,x>0,求导数判断单调性求出极值,转化为g(x)max≤0即可.
(1)f′(x)![]() ,x>0,
,x>0,
令f′(x)=0得,x=e,
在(0.e)上,f′(x)>0,即f(x)单调递增;
在(e,+∞)上,f′(x)<0,即f(x)单调递减.
故f(x)在(0,e)单调递增,在(e,+∞)上单调递减,
(2)当a>0时,设g(x)=f(x)﹣b![]() ,x>0,
,x>0,
∴g′(x)![]() ,
,
令g′(x)=0,得x=1,
当0<x<1时,g′(x)>0,即g(x)单调递增,
当x>1时,g′(x)<0,即g(x)单调递减,
∴g(x)max=g(1)=a﹣b.
要使不等式![]() 恒成立,
恒成立,
只需g(x)max≤0,
即a﹣b≤0,
∴a≤b.
故实数a,b的大小关系为:a≤b.


科目:高中数学 来源: 题型:
【题目】某厂生产某种产品的年固定成本为250万元,每生产![]() 千件,需另投入成本
千件,需另投入成本![]() ,当年产量不足80千件时,
,当年产量不足80千件时,![]() (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,![]() (万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(万元),每件售价为0.05万元,通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4cosωxsin(ωx![]() )(ω>0)的最小正周期是π.
)(ω>0)的最小正周期是π.
(1)求函数f(x)在区间(0,π)上的单调递增区间;
(2)若f(x0)![]() ,x0∈[
,x0∈[![]() ,
,![]() ],求cos2x0的值.
],求cos2x0的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=tan(ωx+φ)(ω>0,0<φ<![]() ),已知函数y=f(x)的图象与x轴相邻两个交点的距离为
),已知函数y=f(x)的图象与x轴相邻两个交点的距离为![]() ,且图象关于点M(-
,且图象关于点M(-![]() ,0)对称.
,0)对称.
(1)求f(x)的解析式;
(2)求f(x)的单调区间;
(3)求不等式-1≤f(x)≤![]() 的解集.
的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数
是奇函数
(Ⅰ)求![]() 值;
值;
(Ⅱ)判断并证明该函数在定义域![]() 上的单调性;
上的单调性;
(Ⅲ)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅳ)设关于![]() 的函数
的函数![]() 有零点,求实数
有零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
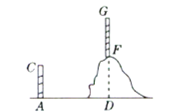
【题目】如图,要测量山顶上的电视塔FG的高度,已知山的西面有一栋楼AC(该楼的高度低于山的高度).试设计在楼AC上测山顶电视塔高度的测量、计算方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com