分析:满足条件的点(x,y)的区域为△OAB及其内部区域,如图所示,目标函数z=log2xy+1,函数t=xy表示以x、y为长和宽的矩形的面积,故点A的坐标满足使函数t=xy取得最大值,此时,x=1,y=2,求得t的最大值,可得z的最大值.
解答: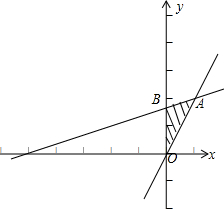
解:∵正数x、y满足
,
故满足条件的点(x,y)的区域为△OAB及其内部区域,如图所示:
目标函数z=log
2x+log
2y+1=log
2xy+1,
故只有函数t=xy取得最大值时,z才取得最大值.
而函数t=xy表示以x、y为长和宽的矩形的面积,易得A(1,2)、B(0,
),
故点A的坐标为最优解,满足使函数t=xy取得最大值,此时,x=1,y=2,
∴t
max=1×2=2,故z的最大值为log
22+1=2,
故选:B.
点评:本题主要考查简单的线性规划问题,体现了数形结合以及转化的数学思想.

 解:∵正数x、y满足
解:∵正数x、y满足

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案