练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某家具厂有方木料，五合板，准备加工成书桌和书橱出售.已知生产每张书桌需要方木料、五合板；生产每个书橱需要方木枓、五合板.出售一张书桌可获利润元，出售一个书橱可获利润元，怎样安排生产可使所得利润最大？最大利润为多少？

    【答案】生产书桌张，书橱个，可使所得利润最大，最大利润为元.

    【解析】【试题分析】本题旨在考查线性规划的知识在解决实际问题中的运用，求解时充分借助题设条件，将问题转化为二元一次不等式组，然后画出不等式组表示的区域，然后数形结合求解：

    解：

    设生产书桌张，书橱个，利润总额为元.则，可行域如图.由图可知：当直线经过可行域上的点时，截距最大，即最大，解方程组得的坐标为， （元）.因此，生产书桌张，书橱个，可使所得利润最大，最大利润为元.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知直线l1：（1+4k）x﹣（2﹣3k）y+（2﹣14k）=0，圆C：x2+y2﹣6x﹣8y+9=0．
    （1）判断直线l1与圆的位置关系，并证明你的结论；
    （2）直线l2过直线l1的定点且l1⊥l2 ， 若l1与圆C交与A，B两点，l2与圆C交与E，F两点，求AB+EF的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知Sn为数列{an}的前n项和，an＞0，an2+2an=4Sn﹣1．
    （1）求{an}的通项公式；
    （2）设bn= ，求{bn}的前n项和Tn ．
    （3）cn= ，{cn}的前n项和为Dn ， 求证：Dn＜ ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】袋中共有8个球，其中3个红球、2个白球、3个黑球．若从袋中任取3个球，则所取3个球中至多有1个红球的概率是（ ）
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在四面体ABCD中，E，F分别是AC，BD的中点，若AB=2，CD=4，EF⊥AB，则EF与CD所成的角的度数为（ ）
    A.90°
    B.45°
    C.60°
    D.30°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知单调递增的等比数列满足，且是， 的等差中项.

    （Ⅰ）求数列的通项公式；

    （Ⅱ）若数列满足，求数列的通项公式；

    （Ⅲ）在（Ⅱ）的条件下，设，问是否存在实数使得数列（）是单调递增数列？若存在，求出的取值范围；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1，2，在Rt△ABC中，AB=BC=4，点E在线段AB上，过点E作交AC于点F，将△AEF沿EF折起到△PEF的位置（点A与P重合），使得∠PEB=60°．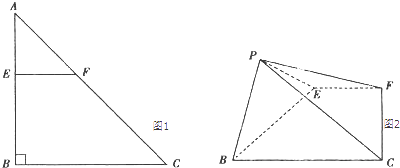

    （1）求证：EF⊥PB；
    （2）试问：当点E在何处时，四棱锥P﹣EFCB的侧面的面积最大？并求此时四棱锥P﹣EFCB的体积及直线PC与平面EFCB所成角的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设点Pi（xi ， yi）在直线li：aix+biy=ci上，若ai+bi=ici（i=1，2），且|P1P2|≥ 恒成立，则 + = ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知向量 =（1，sinx）， =（cos（2x+ ），sinx），函数f（x）= ﹣ cos2x
    （1）求函数f（x）的解析式及其单调递增区间；
    （2）当x∈[0， ]时，求函数f（x）的值域．

    查看答案和解析>>

    同步练习册答案