
观察下列等式:13+23=(1+2)2,13+23+33=(1+2+3)2,13+23+33+43=
(1+2+3+4)2,…,根据上述规律,第四个等式为.
(3)
解 (1)f’(x)=![]()
![]() ,g’(x)=
,g’(x)=![]() (x>0),
(x>0),
![]() 由已知得
由已知得 ![]() =alnx,
=alnx,
![]() =
=![]() , 解德a=
, 解德a=![]() ,x=e2,
,x=e2,
![]() 两条曲线交点的坐标为(e2,e) 切线的斜率为k=f’(e2)=
两条曲线交点的坐标为(e2,e) 切线的斜率为k=f’(e2)= ![]() ,
,
![]() 切线的方程为y-e=
切线的方程为y-e=![]() (x- e2).
(x- e2).
(2)由条件知![]()
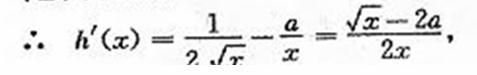
Ⅰ 当a.>0时,令h ![]() (x)=0,解得x=
(x)=0,解得x=![]() ,
,
所以当0 < x< ![]() 时 h
时 h ![]() (x)<0,h(x)在(0,
(x)<0,h(x)在(0,![]() )上递减;
)上递减;
当x>![]() 时,h
时,h ![]() (x)>0,h(x)在(0,
(x)>0,h(x)在(0,![]() )上递增。
)上递增。
所以x>![]() 是h(x)在(0, +∞ )上的唯一极致点,且是极小值点,从而也是h(x)的最小值点。
是h(x)在(0, +∞ )上的唯一极致点,且是极小值点,从而也是h(x)的最小值点。
所以Φ (a)=h(![]() )= 2a-aln
)= 2a-aln![]() =2
=2
Ⅱ当a ≤ 0时,h(x)=(1/2-2a) /2x>0,h(x)在(0,+∞)递增,无最小值。
故 h(x) 的最小值Φ (a)的解析式为2a(1-ln2a) (a>o)
(3)由(2)知Φ (a)=2a(1-ln2a)
则 Φ 1(a )=-2ln2a,令Φ 1(a )=0 解得 a =1/2
当 0<a<1/2时,Φ 1(a )>0,所以Φ (a ) 在(0,1/2) 上递增
当 a>1/2 时, Φ 1(a )<0,所以Φ(a ) 在 (1/2, +∞)上递减。
所以Φ(a )在(0, +∞)处取得极大值Φ(1/2 )=1
因为Φ(a )在(0, +∞)上有且只有一个极致点,所以Φ(1/2)=1也是Φ(a)的最大值
所当a属于 (0, +∞)时,总有Φ(a) ≤ 1


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 2 |
| 3 |
| 7 |
| 3 |
| 8 |
| 3 |
| 10 |
| 3 |
| 11 |
| 3 |
| 16 |
| 3 |
| 17 |
| 3 |
| 19 |
| 3 |
| 20 |
| 3 |
| 22 |
| 3 |
| 23 |
| 3 |
| 3n+1 |
| 3 |
| 3n+2 |
| 3 |
| 3m-2 |
| 3 |
| 3m-1 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com