
【题目】已知数列{an}的各项均为正,Sn为数列{an}的前n项和,an2+2an=4Sn+3.
(1)求{an}的通项公式;
(2)设bn![]() ,求数列{bn}的前n项和.
,求数列{bn}的前n项和.
【答案】(1)an=2n+1;(2)2![]() .
.
【解析】
(1)根据题意求出首项,再由(an+12+2an+1)﹣(an2+2an)=4an+1,求得该数列为等差数列即可求得通项公式;
(2)利用错位相减法进行数列求和.
(1)∵an2+2an=4Sn+3,
∴a12+2a1=4S1+3,即![]() ,
,
解得:a1=3或a1=﹣1(舍),
又∵an+12+2an+1=4Sn+1+3,
∴(an+12+2an+1)﹣(an2+2an)=4an+1,
整理得:(an+1﹣an)(an+1+an)=2(an+1+an),
又∵数列{an}的各项均为正,
∴an+1﹣an=2,
∴数列{an}是首项为3、公差为2的等差数列,
∴数列{an}的通项公式an=3+2(n﹣1)=2n+1;
(2)由(1)可知bn![]() ,
,
记数列{bn}的前n项和为Tn,则
Tn=3![]() 5
5![]() (2n+1)
(2n+1)![]() ,
,
![]() Tn=3
Tn=3![]() 5
5![]() …+(2n﹣1)
…+(2n﹣1)![]() (2n+1)
(2n+1)![]() ,
,
错位相减得:![]() Tn=1+2(
Tn=1+2(![]()
![]() )﹣(2n+1)
)﹣(2n+1)![]()
=12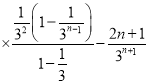
![]() ,
,
∴Tn![]() (
(![]() )=2
)=2![]() .
.


科目:高中数学 来源: 题型:
【题目】美团外卖和百度外卖两家公司其“骑手”的日工资方案如下:美团外卖规定底薪70元,每单抽成1元;百度外卖规定底薪100元,每日前45单无抽成,超出45单的部分每单抽成6元,假设同一公司的“骑手”一日送餐单数相同,现从两家公司个随机抽取一名“骑手”并记录其100天的送餐单数,得到如下条形图:
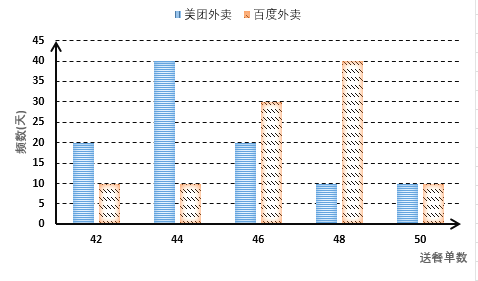
(Ⅰ)求百度外卖公司的“骑手”一日工资![]() (单位:元)与送餐单数
(单位:元)与送餐单数![]() 的函数关系;
的函数关系;
(Ⅱ)若将频率视为概率,回答下列问题:
①记百度外卖的“骑手”日工资为![]() (单位:元),求
(单位:元),求![]() 的分布列和数学期望;
的分布列和数学期望;
②小明拟到这两家公司中的一家应聘“骑手”的工作,如果仅从日收入的角度考虑,请你利用所学的统计学知识为他作出选择,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年3月20日是国际幸福日,某电视台随机调查某一社区人们的幸福度.现从该社区群中随机抽取18名,用“10分制”记录了他们的幸福度指数,结果见如图所示茎叶图,其中以小数点前的一位数字为茎,小数点后的一位数字为叶.若幸福度不低于8.5分,则称该人的幸福度为“很幸福”.
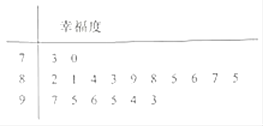
(Ⅰ)求从这18人中随机选取3人,至少有1人是“很幸福”的概率;
(Ⅱ)以这18人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记![]() 表示抽到“很幸福”的人数,求
表示抽到“很幸福”的人数,求![]() 的分布列及
的分布列及![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
甲、乙、丙三名射击运动员射中目标的概率分别为![]()
![]() ,三人各射击一次,击中目标的次数记为
,三人各射击一次,击中目标的次数记为![]() .
.
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)在概率![]() (
(![]() =0,1,2,3)中, 若
=0,1,2,3)中, 若![]() 的值最大, 求实数
的值最大, 求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位计划在一水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和,单位:亿立方米)都在40以上,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和,单位:亿立方米)都在40以上,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
(1)求未来3年中,设![]() 表示流量超过120的年数,求
表示流量超过120的年数,求![]() 的分布列及期望;
的分布列及期望;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电机最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5000万元,若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代中的“礼、乐、射、御、书、数”合称“六艺”.“礼”,主要指德育;“乐”,主要指美育;“射”和“御”,就是体育和劳动;“书”,指各种历史文化知识;“数”,指数学.某校国学社团开展“六艺”课程讲座活动,每艺安排一节,连排六节,一天课程讲座排课有如下要求:“数”必须排在第三节,且“射”和“御”两门课程相邻排课,则“六艺”课程讲座不同的排课顺序共有( )
A.12种B.24种C.36种D.48种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com