
分析 根据向量的数量积运算和模的运算,以及向量垂直的条件得$\overrightarrow{a}•\overrightarrow{b}$=$\frac{66}{7}$,再根据向量的夹角公式计算即可.
解答 解:∵|$\overrightarrow{a}$|=4,|$\overrightarrow{b}$|=3,
∵(3$\overrightarrow{a}$-$\overrightarrow{b}$)⊥($\overrightarrow{a}$-2$\overrightarrow{b}$),
∴(3$\overrightarrow{a}$-$\overrightarrow{b}$)•($\overrightarrow{a}$-2$\overrightarrow{b}$)=0,
∴3|$\overrightarrow{a}$|2+2|$\overrightarrow{b}$|2-7($\overrightarrow{a}•\overrightarrow{b}$)=0,
∴$\overrightarrow{a}•\overrightarrow{b}$=$\frac{66}{7}$,
设$\overrightarrow{a}$与$\overrightarrow{b}$夹角为θ,
∴cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{\frac{66}{7}}{4×3}$=$\frac{11}{14}$.
点评 本题考查平面向量的坐标运算和数量积判断两个平面垂直条件的灵活运用,解题时要认真审题,仔细解答.是基础题


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:选择题
 如图△A′B′C′是△ABC的直观图,其中A′B′=A′C,那么△ABC是( )
如图△A′B′C′是△ABC的直观图,其中A′B′=A′C,那么△ABC是( )| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 钝角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
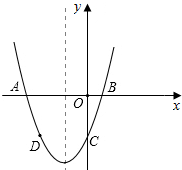 已知二次函数y=x2+bx+c的图象过点A(-3,0)和点B(1,0),且与y轴交于点C,D点在抛物线上且横坐标是-2.
已知二次函数y=x2+bx+c的图象过点A(-3,0)和点B(1,0),且与y轴交于点C,D点在抛物线上且横坐标是-2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{2}{3}$ | C. | -2 | D. | -4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com