
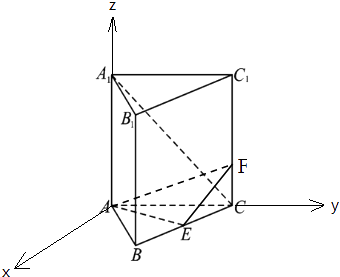
【题目】(用空间向量坐标表示解答)已知正三棱柱ABC﹣A1B1C1的各棱长都是4,E是BC的中点,F在CC1上,且CF=1. 
(1)求证:EF⊥A1C;
(2)求二面角C﹣AF﹣E的平面角的余弦值.
【答案】
(1)证明:以A为原点,在平面ABC中过A作AC的垂线为x轴,AC为y轴,AA1为z轴,
建立空间直角坐标系,
B(2 ![]() ,2,0),C(0,4,0),E(
,2,0),C(0,4,0),E( ![]() ,3,0),F(0,4,1),A1(0,0,4),
,3,0),F(0,4,1),A1(0,0,4),
![]() =(﹣
=(﹣ ![]() ,1,1),
,1,1), ![]() =(0,4,﹣4),
=(0,4,﹣4),
![]()
![]() =0+4﹣4=0,
=0+4﹣4=0,
∴EF⊥A1C.
(2)解: ![]() =(
=( ![]() ),
), ![]() =(0,4,1),
=(0,4,1),
设平面AEF的法向量 ![]() =(x,y,z),
=(x,y,z),
则 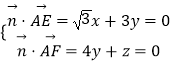 ,取x=
,取x= ![]() ,得
,得 ![]() =(
=( ![]() ),
),
平面ACF的法向量 ![]() =(1,0,0),
=(1,0,0),
设二面角C﹣AF﹣E的平面角为θ,
则cosθ= ![]() =
= ![]() =
= ![]() .
.
∴二面角C﹣AF﹣E的平面角的余弦值为 ![]() .
.
【解析】(1)以A为原点,在平面ABC中过A作AC的垂线为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,利用向量法能证明EF⊥A1C.(2)求出平面AEF的法向量和平面ACF的法向量,利用向量法能求出二面角C﹣AF﹣E的平面角的余弦值.
【考点精析】解答此题的关键在于理解空间中直线与直线之间的位置关系的相关知识,掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣3x+2=0},B={x|x2﹣ax+a﹣1=0},C={x|x2﹣mx+2=0}.若A∪B=A,A∩C=C,求实数a,m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一艘船在航行过程中发现前方的河道上有一座圆拱桥.在正常水位时,拱桥最高点距水面8m,拱桥内水面宽32m,船只在水面以上部分高6.5m,船顶部宽8m,故通行无阻,如图所示. 
(1)建立适当的平面直角坐标系,求正常水位时圆弧所在的圆的方程;
(2)近日水位暴涨了2m,船已经不能通过桥洞了.船员必须加重船载,降低船身在水面以上的高度,试问:船身至少降低多少米才能通过桥洞?(精确到0.1m, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2﹣2x+c,且f(x)>0的解集是 ![]() .
.
(1)求f(2)的最小值及f(2)取最小值时f(x)的解析式;
(2)在f(2)取得最小值时,若对于任意的x>2,f(x)+4≥m(x﹣2)恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆中心是原点O,它的短轴长为 ![]() ,右焦点F(c,0)(c>0),它的长轴长为2a(a>c>0),直线l:
,右焦点F(c,0)(c>0),它的长轴长为2a(a>c>0),直线l: ![]() 与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.
与x轴相交于点A,|OF|=2|FA|,过点A的直线与椭圆相交于P、Q两点.
(1)求椭圆的方程和离心率;
(2)若 ![]() ,求直线PQ的方程;
,求直线PQ的方程;
(3)设 ![]() (λ>1),过点P且平行于直线l的直线与椭圆相交于另一点M,证明:
(λ>1),过点P且平行于直线l的直线与椭圆相交于另一点M,证明: ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面ABEF⊥平面ABC,四边形ABEF为矩形,AC=BC.O为AB的中点,OF⊥EC. 
(1)求证:OE⊥FC:
(2)若 ![]() 时,求二面角F﹣CE﹣B的余弦值.
时,求二面角F﹣CE﹣B的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com