
【题目】已知函数![]() .
.
(1)若![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 平行,求
平行,求![]() 的值;
的值;
(2)若![]() ,且函数
,且函数![]() 的值域为
的值域为![]() ,求
,求![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
【题目】母线长为![]() ,底面半径为
,底面半径为![]() 的圆锥内有一球
的圆锥内有一球![]() ,与圆锥的侧面、底面都相切,现放入一些小球,小球与圆锥底面、侧面、球
,与圆锥的侧面、底面都相切,现放入一些小球,小球与圆锥底面、侧面、球![]() 都相切,这样的小球最多可放入__________个.
都相切,这样的小球最多可放入__________个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() 是
是![]() 边上异于端点的动点,
边上异于端点的动点,![]() 于点
于点![]() ,将矩形
,将矩形![]() 沿
沿![]() 折叠至
折叠至![]() 处,使面
处,使面![]() 面
面![]() .点
.点![]() 分别为
分别为![]() 的中点.
的中点.
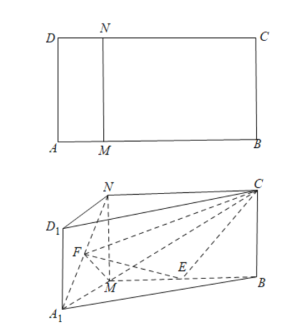
(1)证明:![]() //面
//面![]() ;
;
(2)设![]() ,当x为何值时,四面体
,当x为何值时,四面体![]() 的体积最大,并求出最大值.
的体积最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)和y=g(x)在[-2,2]的图像如图所示,给出下列四个命题:

①方程f[g(x)]=0有且仅有6个根
②方程g[f(x)]=0有且仅有3个根
③方程f[f(x)]=0有且仅有5个根
④方程g[g(x)]=0有且仅有4个根
其中正确的命题是___
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过双曲线![]() 的右焦点
的右焦点![]() 作直线
作直线![]() ,且直线
,且直线![]() 与双曲线
与双曲线![]() 的一条渐近线垂直,垂足为
的一条渐近线垂直,垂足为![]() ,直线
,直线![]() 与另一条渐近线交于点
与另一条渐近线交于点![]() ,已知
,已知![]() 为坐标原点,若
为坐标原点,若![]() 的内切圆的半径为
的内切圆的半径为![]() ,则双曲线
,则双曲线![]() 的离心率为( )
的离心率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或2
或2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究国民收入在国民之间的分配,避免贫富过分悬殊,美国统计学家劳伦茨提出了著名的劳伦茨曲线,如图所示.劳伦茨曲线为直线![]() 时,表示收入完全平等,劳伦茨曲线为折线
时,表示收入完全平等,劳伦茨曲线为折线![]() 时,表示收入完全不平等.记区域
时,表示收入完全不平等.记区域![]() 为不平等区域,
为不平等区域,![]() 表示其面积,
表示其面积,![]() 为
为![]() 的面积.将
的面积.将![]() ,称为基尼系数.对于下列说法:
,称为基尼系数.对于下列说法:
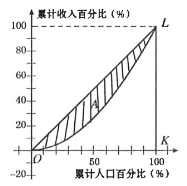
①![]() 越小,则国民分配越公平;
越小,则国民分配越公平;
②设劳伦茨曲线对应的函数为![]() ,则对
,则对![]() ,均有
,均有![]() ;
;
③若某国家某年的劳伦茨曲线近似为![]() ,则
,则![]() ;
;
其中正确的是:( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com