
【题目】设函数![]() .若曲线
.若曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为
![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)求函数![]() 的单调区间;
的单调区间;
(2)若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) 函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]()
(2) ![]()
【解析】试题分析:(1)第(1)问,先根据曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为
![]() 求出m=1,n=0,再利用导数求函数f(x)的单调区间.(2)第(2)问,先把原命题转化为函数
求出m=1,n=0,再利用导数求函数f(x)的单调区间.(2)第(2)问,先把原命题转化为函数![]() 对任意
对任意![]() 恒成立,再利用导数求函数H(x)的单调性,检验每一种情况下H(x)的最大值是否小于零.
恒成立,再利用导数求函数H(x)的单调性,检验每一种情况下H(x)的最大值是否小于零.
试题解析:
(1)函数![]() 定义域为
定义域为![]() .
.![]() 得
得![]() ,
,
![]() ,即
,即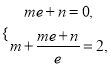 所以
所以![]() .所以
.所以![]() ,
,
![]() .函数
.函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() .
.
(2)由题得函数![]() 对任意
对任意![]() 恒成立,
恒成立,
即不等式![]() 对任意
对任意![]() 恒成立.
恒成立.
又![]() ,当
,当![]() 即
即![]() 恒成立时,
恒成立时,
函数![]() 递减,设
递减,设![]() ,则
,则![]() ,所以
,所以![]() ,即
,即![]() ,符合题意;
,符合题意;
当![]() 时,
时, ![]() 恒成立,此时函数
恒成立,此时函数![]() 单调递增.于是不等式
单调递增.于是不等式![]() 对任意
对任意![]() 恒成立,不符合题意;
恒成立,不符合题意;
当![]() 时,设
时,设![]() ,
,
则![]()
![]() ;
;
当![]() 时,
时, ![]() ,此时
,此时![]() 单调递增,
单调递增,
![]()
![]() ,
,
故当![]() 时,函数
时,函数![]() 递增.于是当
递增.于是当![]() 时,
时, ![]() 成立,不符合题意;
成立,不符合题意;
综上所述,实数![]() 的取值范围为:
的取值范围为: ![]() .
.
点睛:本题的难点在于得到![]() 后如何解不等式
后如何解不等式![]() >0或
>0或![]() <0,只有解出了不等式才能得到函数H(x)的单调区间.本题利用了再构造再求导的方法(即二次求导).当我们求出函数f(x)的导数
<0,只有解出了不等式才能得到函数H(x)的单调区间.本题利用了再构造再求导的方法(即二次求导).当我们求出函数f(x)的导数![]() 之后,如果
之后,如果![]() 不易解出,可以利用二次求导找不等式的解集,从而找到原函数的单调性.
不易解出,可以利用二次求导找不等式的解集,从而找到原函数的单调性.


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以O为极点,x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ=2(cos θ+sin θ).
(1)求C的直角坐标方程;
(2)直线l: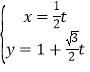 (t为参数)与曲线C交于A,B两点,与y轴交于点E,求|EA|+|EB|.
(t为参数)与曲线C交于A,B两点,与y轴交于点E,求|EA|+|EB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E的方程: ![]() ,P为椭圆上的一点(点P在第三象限上),圆P 以点P为圆心,且过椭圆的左顶点M与点C(﹣2,0),直线MP交圆P与另一点N.
,P为椭圆上的一点(点P在第三象限上),圆P 以点P为圆心,且过椭圆的左顶点M与点C(﹣2,0),直线MP交圆P与另一点N. 
(1)求圆P的标准方程;
(2)若点A在椭圆E上,求使得 ![]() 取得最小值的点A的坐标;
取得最小值的点A的坐标;
(3)若过椭圆的右顶点的直线l上存在点Q,使∠MQN为钝角,求直线l斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,且函数g(x)=loga(x2+x+2)(a>0,且a≠1)在[﹣
,且函数g(x)=loga(x2+x+2)(a>0,且a≠1)在[﹣ ![]() ,1]上的最大值为2,若对任意x1∈[﹣1,2],存在x2∈[0,3],使得f(x1)≥g(x2),则实数m的取值范围是( )
,1]上的最大值为2,若对任意x1∈[﹣1,2],存在x2∈[0,3],使得f(x1)≥g(x2),则实数m的取值范围是( )
A.(﹣∞,﹣ ![]() ]
]
B.(﹣∞, ![]() ]
]
C.[ ![]() ,+∞)
,+∞)
D.[﹣ ![]() ,+∞]
,+∞]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,我国PM2.5标准采用世界卫生组织设定的最宽限值,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.
某试点城市环保局从该市市区2016年全年每天的PM2.5监测数据中随机抽取6天的数据作为样本,监测值茎叶图(十位为茎,个位为叶)如图所示,若从这6天的数据中随机抽出2天,

(1)求恰有一天空气质量超标的概率;
(2)求至多有一天空气质量超标的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求函数y=![]() 的值的程序框图如图所示.
的值的程序框图如图所示.
(1)指出程序框图中的错误,并写出算法;
(2)重新绘制解决该问题的程序框图,并回答下面提出的问题.
①要使输出的值为正数,输入的x的值应满足什么条件?
②要使输出的值为8,输入的x值应是多少?
③要使输出的y值最小,输入的x值应是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com