
分析 函数f(x)=2x(x+a)-1在区间[0,1]上有零点?方程x+a=$(\frac{1}{2})^{x}$在区间[0,1]上有解.?函数y=x+a,y=$\frac{1}{{2}^{x}}$的图象在区间[0,1]上有交点.如图在同一坐标系内画出函数y=x+a,y=$\frac{1}{{2}^{x}}$的图象,结合图象可得
解答  解:函数f(x)=2x(x+a)-1在区间[0,1]上有零点?方程x+a=$(\frac{1}{2})^{x}$在区间[0,1]上有解.
解:函数f(x)=2x(x+a)-1在区间[0,1]上有零点?方程x+a=$(\frac{1}{2})^{x}$在区间[0,1]上有解.
?函数y=x+a,y=$\frac{1}{{2}^{x}}$的图象在区间[0,1]上有交点.
如图在同一坐标系内画出函数y=x+a,y=$\frac{1}{{2}^{x}}$的图象,结合图象可得:
0+a≤($\frac{1}{2}$)0,且1+a≥($\frac{1}{2}$)1⇒-$\frac{1}{2}$≤a≤1
实数a的取值范围是[-$\frac{1}{2}$,1]
故答案为:[-$\frac{1}{2}$,1]
,
点评 本题考查了函数的零点,函数与方程思想、数形结合思想,属于中档题.


科目:高中数学 来源: 题型:解答题
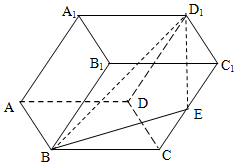 已知斜四棱柱平面ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,
已知斜四棱柱平面ABCD-A1B1C1D1的各棱长均为2,∠A1AD=60°,∠BAD=90°,平面A1ADD1⊥平面ABCD,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
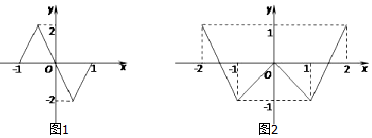
| A. | 14 | B. | 12 | C. | 10 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | [0,1] | C. | (1,3) | D. | [1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
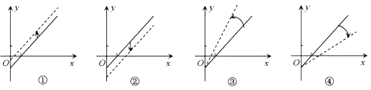
| A. | ①反映了建议(Ⅱ),③反映了建议(Ⅰ) | B. | ①反映了建议(Ⅰ),③反映了建议(Ⅱ) | ||
| C. | ②反映了建议(Ⅰ),④反映了建议(Ⅱ) | D. | ④反映了建议(Ⅰ),②反映了建议(Ⅱ) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com