
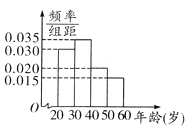
【题目】某工厂有120名工人,其年龄都在20~ 60岁之间,各年龄段人数按[20,30),[30,40),[40,50),[50,60]分成四组,其频率分布直方图如下图所示.工厂为了开发新产品,引进了新的生产设备,要求每个工人都要参加A、B两项培训,培训结束后进行结业考试。已知各年龄段两项培训结业考试成绩优秀的人数如下表所示。假设两项培训是相互独立的,结业考试也互不影响。
年龄分组 | A项培训成绩 优秀人数 | B项培训成绩 优秀人数 |
[20,30) | 27 | 16 |
[30,40) | 28 | 18 |
[40,50) | 16 | 9 |
[50,60] | 6 | 4 |
(1)若用分层抽样法从全厂工人中抽取一个容量为40的样本,求四个年龄段应分别抽取的人数;
(2)根据频率分布直方图,估计全厂工人的平均年龄;
(3)随机从年龄段[20,30)和[40,50)中各抽取1人,设这两人中A、B两项培训结业考试成绩都优秀的人数为X,求X的分布列和数学期望.
【答案】(1)12,14,8,6;(2)37岁;(3)见解析.
【解析】分析:(1)由频率分布直方图得各年龄段的频率,分别乘以40即可得人数;
(2)将各年龄段的中点值乘以频率累加可得平均年龄;
(3)先分别计算年龄在[20,30)和年龄段[40,50)的工人A、B两项培训结业考试成绩都优秀的概率,由题设知,X的可能取值为0,1,2,进而求概率可得分布列,利用期望公式可得期望.
详解:(1)由频率分布直方图可知,年龄段[20,30),[30,40),[40,50),[50,60]的人数的频率分别为0.3,0.35,0.2,0.15.
因为40×0.3=12,40×0.35 =14,40×0.2=8,40×0.15 =6,
所以年龄段[20,30),[30,40),[40,50),[50,60]应抽取人数分别为12,14,8,6.
(2)因为各年龄段的中点值分别为25,35,45,55,对应的频率分别为0.3,0.35,0.2,0.15,则25×0.3+35×0.35 +45×0.2+55×0.15= 37.由此估计全厂工人的平均年龄约为37岁.
(3)因为年龄在[20,30)的工人数为120×0.3=36,从该年龄段任取1人,由表知,此人A项培训结业考试成绩优秀的概率为![]() ,B项培训结业考试成绩优秀的概率为
,B项培训结业考试成绩优秀的概率为![]() ,
,
所以A、B两项培训结业考试成绩都优秀的概率为![]() .
.
因为年龄段[40,50)的工人数为120×0.2=24,从该年龄段任取1人,由表知,此人A项培训结业考试成绩优秀的概率为![]() ,B项培训结业考试成绩优秀的概率为
,B项培训结业考试成绩优秀的概率为![]() ,所以A、B两项培训结业考试成绩都优秀的概率为
,所以A、B两项培训结业考试成绩都优秀的概率为![]() .
.
由题设知,X的可能取值为0,1,2.
其中![]() ,
,
![]() ,
,
![]() ,
,
所以X的分布列如下表:
X | 0 | 1 | 2 |
P |
|
|
|
所以![]() .
.


科目:高中数学 来源: 题型:
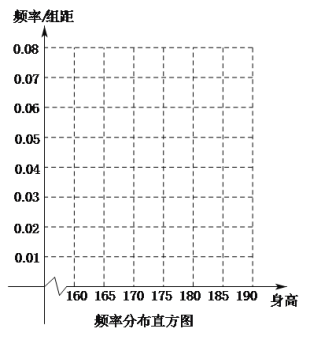
【题目】某电视节目为选拔出现场录制嘉宾,在众多候选人中随机抽取100名选手,按选手身高分组,得到的频率分布表如图所示.
(Ⅰ)请补充频率分布表中空白位置相应数据,再在答题纸上完成下列频率分布直方图;
(Ⅱ)为选拔出舞台嘉宾,决定在第3、4、5组中用分层抽样抽取6人上台,求第3、4、5组每组各抽取多少人?
(Ⅲ)在(Ⅱ)的前提下,电视节目主持人会在上台6人中随机抽取2人表演节目,求第4组至少有一人被抽取的概率?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图(1),平面五边形![]() 中,
中,![]() 为正三角形,
为正三角形,![]() ,
,![]() ,
,![]() .如图(2)将
.如图(2)将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() .点
.点![]() 为线段
为线段![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)若异面直线![]() 与
与![]() 所成角的正切值为
所成角的正切值为![]() ,
,![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个班级,一次数学考试的分数排序如下:
甲班 51 54 59 60 64 68 68 68 70 71
72 72 74 76 77 78 79 79 80 80
82 85 85 86 86 87 87 87 88 89
90 90 91 96 97 98 98 98 100 100
乙班 61 63 63 66 70 71 71 73 75 75
76 79 79 80 80 80 81 81 82 82
83 83 83 84 84 84 85 85 85 85
85 85 86 87 87 88 90 91 94 98
请你就这次考试成绩,对两个班级的数学学习情况进行评价
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解中学生课余观看热门综艺节目“爸爸去哪儿”是否与性别有关,某中学一研究性学习小组从该校学生中随机抽取了![]() 人进行问卷调查.调查结果表明:女生中喜欢观看该节目的占女生总人数的
人进行问卷调查.调查结果表明:女生中喜欢观看该节目的占女生总人数的![]() ,男生喜欢看该节目的占男生总人数的
,男生喜欢看该节目的占男生总人数的![]() .随后,该小组采用分层抽样的方法从这
.随后,该小组采用分层抽样的方法从这![]() 份问卷中继续抽取了
份问卷中继续抽取了![]() 份进行重点分析,知道其中喜欢看该节目的有
份进行重点分析,知道其中喜欢看该节目的有![]() 人.
人.
(1) 现从重点分析的![]() 人中随机抽取了
人中随机抽取了![]() 人进行现场调查,求这两人都喜欢看该节目的概率;
人进行现场调查,求这两人都喜欢看该节目的概率;
(2) 若有![]() 的把握认为“爱看该节目与性别有关”,则参与调查的总人数
的把握认为“爱看该节目与性别有关”,则参与调查的总人数![]() 至少为多少?
至少为多少?
参考数据:
| 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.
(Ⅰ)求证:PA∥平面BDE;
(Ⅱ)平面PAC⊥平面BDE;
(Ⅲ)若二面角E-BD-C为30°,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司对以下两个项目进行前期市场调研:项目![]() :通信设备.根据调研,投资到该项目上,所有可能结果为:获利
:通信设备.根据调研,投资到该项目上,所有可能结果为:获利![]() 、损失
、损失![]() 、不赔不赚,且这三种情况发生的概率分别为
、不赔不赚,且这三种情况发生的概率分别为![]() ;项目
;项目![]() :新能源汽车.根据调研,投资到该项目上,所有可能结果为:获利
:新能源汽车.根据调研,投资到该项目上,所有可能结果为:获利![]() 、亏损
、亏损![]() ,且这两种情况发生的概率分别为
,且这两种情况发生的概率分别为![]() .经测算,当投入
.经测算,当投入![]() 两个项目的资金相等时,它们所获得的平均收益(即数学期望)也相等.
两个项目的资金相等时,它们所获得的平均收益(即数学期望)也相等.
(1)求![]() 的值;
的值;
(2)若将![]() 万元全部投到其中的一个项目,请你从投资回报稳定性考虑,为投资公司选择一个合理的项目,并说明理由.
万元全部投到其中的一个项目,请你从投资回报稳定性考虑,为投资公司选择一个合理的项目,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂人员及工资构成如下表:
人员 | 经理 | 管理人员 | 高级技工 | 工人 | 学徒 | 合计 |
周工资/元 | 2200 | 1250 | 1220 | 1200 | 490 | |
人数 | 1 | 6 | 5 | 10 | 1 | 23 |
(1)指出这个问题中的众数、中位数、平均数.
(2)这个问题中,平均数能客观地反映该工厂的工资水平吗?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com