
科目:高中数学 来源:不详 题型:解答题
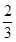 和
和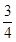 假设两人射击是否击中目标,相互
假设两人射击是否击中目标,相互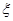 表示甲击中目标时射击的次数,求
表示甲击中目标时射击的次数,求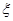 的数学期望
的数学期望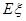 .(结果可以用分数表示)
.(结果可以用分数表示)查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 N),乙也有一只放有3本《周易》,2本《万年历》,1《吴从纪要》的书箱,两人各自从自己的箱子中任取一本书(由于每本书厚薄、大小相近,每本书被抽取出的可能性一样),规定:当两本书同名时甲将被派出去完成某项任务,否则乙去.
N),乙也有一只放有3本《周易》,2本《万年历》,1《吴从纪要》的书箱,两人各自从自己的箱子中任取一本书(由于每本书厚薄、大小相近,每本书被抽取出的可能性一样),规定:当两本书同名时甲将被派出去完成某项任务,否则乙去.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
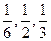 ;9∶00~10∶00到站的客车B可能在9∶10,9∶30,
;9∶00~10∶00到站的客车B可能在9∶10,9∶30, 9∶50到站,其概率依次为
9∶50到站,其概率依次为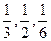 .
.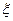 ,求
,求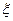 的分布列和
的分布列和 ;
;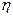 ,求
,求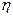 的分布列和
的分布列和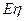 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 分,一名观众随意连线,将他的得分记作ξ.
分,一名观众随意连线,将他的得分记作ξ.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
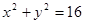 内的次数
内的次数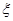 的均值为________
的均值为________查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
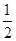 .若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助,令
.若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助,令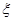 表示该公司的资助总额.
表示该公司的资助总额.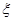 的分布列;
的分布列;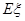 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com