
如图,平面PAD⊥平面ABCD,ABCD为正方形,∠PAD=90°,且PA=AD=2;E、F、G分别是线段PA、PD、CD的中点。
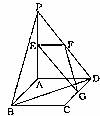
(1)求证:PB//平面EFG;
(2)求异面直线:EG与BD所成的角;
(3)在线段CD上是否存在一点Q,使得A到平面EFQ的距离为![]() ,若存在,求出CQ的值;若不存在,请说明理由。
,若存在,求出CQ的值;若不存在,请说明理由。
解法一:(1)证明:取AB中点H,连结GH,GE,
∵E、F、G分别是线段PA、PD、CD的中点,
∴GH//AD//EF
∴E,F,H,H四点共面,
又H为AB的中点
∴EH//PB。
又EH![]() 面EFG,PB
面EFG,PB![]() 平面EFG,
平面EFG,
∴PB//面EFG。
(2)解:取BC的中点为M,连结GM、AM、EM,则EM//BD,
∴∠EGM(或其补角)就是异面直线EG与BD所成的角
在Rt△MAE中,EM![]()
同理EG=![]()
∴在Rt△MAE中,![]()
故异面直线EG与BD所成的角为![]()
(3)
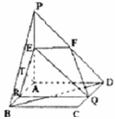
假设在线段CD上存在一点Q满足题设条件,
过点Q作QR⊥AB于R,连结RE,则OQ//AD
∵ABCD是正方形,△PAD是直角三角形,且PA=AD=2,
∴AD⊥AB,AD⊥PA,又AB![]() OA=A,
OA=A,
∴AD⊥平面PAB
又∵E、F分别是PA、PD中点,
∴EF//AD,
∴EF⊥平面PAB又EF![]() 面EFQ,
面EFQ,
∴面EFQ⊥平面PAB,
过A作AT⊥ER于T,则AT⊥面EFQ,
∴AT就是点A到平面EFQ的距离
设CQ![]()
![]()
在Rt△EAR中,AT![]()
解得![]()
故存在点Q,当![]()
解法二:建立如图所示的空间直角坐标系A―xyz
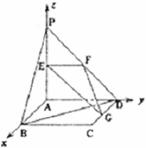
则A(0,0,0),B(2,0,0),C(2,2,0),D(0,2,0)
P(0,0,2),E(0,0,1),F(0,1,1),G(1,2,0)
(1)证明:∵![]()
![]()
即![]()
又∵![]()
∴![]() 共面。
共面。
∵PB![]() 平面EFG,
平面EFG,
∴PB//平面EFG,
(2)解∵![]()
∴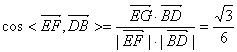
故异面直线EG与BD所成的角为![]()
(3)假设在线段CD上存在一点Q满足题设条件
令![]()
则DQ=2-m
∴点Q的坐标为(2,-m,2,0)
∴![]()
而![]() ,设平面EFQ的法向量为
,设平面EFQ的法向量为![]() ,则
,则
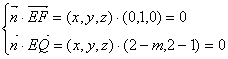
∴![]()
令x=1,则![]()
∴点A到平面EFQ的距离
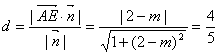
即![]()
∴![]() 不合题意,舍去
不合题意,舍去
故存在点Q,当CQ=![]() 时,点A到平面EFQ的距离为
时,点A到平面EFQ的距离为![]() 。
。


科目:高中数学 来源: 题型:
 18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
18、如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.查看答案和解析>>
科目:高中数学 来源: 题型:
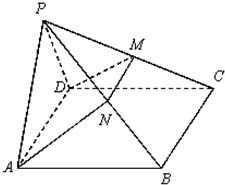 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.查看答案和解析>>
科目:高中数学 来源: 题型:
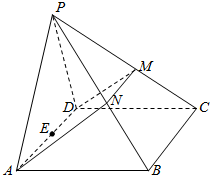 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为4的菱形,且∠BAD=60°,N是PB的中点,过A,D,N的平面交PC于M,E是AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:

图22
(1)求证:EN∥平面PCD;
(2)求证:平面PBC⊥平面ADMN;
(3)求平面PAB与平面ABCD所成二面角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com