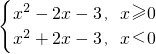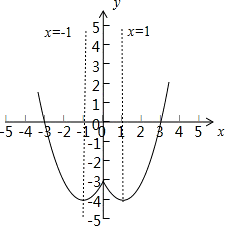已知y=f(x)是R上的偶函数,当x≥0时,f(x)=x2-2x-3.
(1)写出y=f(x)的解析式;
(2)作出y=f(x)的图象;
(3)写出其单调区间及最值.
解:(1)令x<0,则-x>0,
∵当x≥0时,f(x)=x
2-2x-3,
∴f(-x)=(-x)
2-2(-x)-3=x
2+2x-3,
又y=f(x)是R上的偶函数,
∴f(x)=x
2+2x-3(x<0).
∴f(x)=
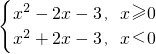
(2)作出其图象如下:
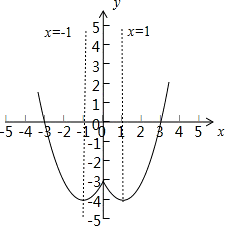
(3)由y=f(x)的图象可知,y=f(x)的单调递减区间为(-∞,-1],[0,1];单调递增区间为[-1,0],[1,+∞);
当x=±1时,y=f(x)取到最小值-4,无最大值.
分析:(1)先求得x<0时的函数解析式,再用分段函数表示出y=f(x)的解析式即可;
(2)y=f(x)是R上的偶函数,其图象关于y轴对称,可先作出当x≥0时,f(x)=x
2-2x-3的图象,关于y轴对称的作出另一侧的图象即可.
(3)由其图象即可写出其单调区间及最值.
点评:本题考查二次函数的图象及性质,考查作图能力与分析转化的能力,属于中档题.