
分析 作函数$f(x)=\left\{\begin{array}{l}{2^{x+1}},x≤0\\{log_2}x,x>0\end{array}\right.$的图象,而[f(x)]2-af(x)=0得f(x)=0或f(x)=a,从而可得f(x)=a有两个解,从而判断.
解答 解:作函数$f(x)=\left\{\begin{array}{l}{2^{x+1}},x≤0\\{log_2}x,x>0\end{array}\right.$的图象如下,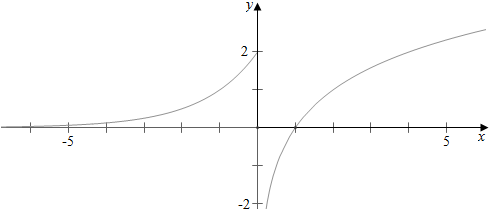 ,
,
∵[f(x)]2-af(x)=0,
∴f(x)=0或f(x)=a,
∴f(x)=0的解为x=1,
∴f(x)=a有两个解,
∴0<a≤2;
故答案为:(0,2].
点评 本题考查了分段函数的应用及数形结合的思想应用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3-i | B. | 2-3i | C. | 3+i | D. | 2+3i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
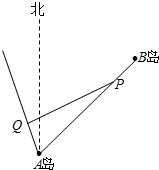 已知海岛B在海岛A的北偏东45°的方向上,两岛相距10海里.小船P从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船Q从海岛A出发,沿北偏西15°方向以4海里/小时的速度移动.
已知海岛B在海岛A的北偏东45°的方向上,两岛相距10海里.小船P从海岛B以2海里/小时的速度沿直线向海岛A移动,同时小船Q从海岛A出发,沿北偏西15°方向以4海里/小时的速度移动.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈R,3x0+$\frac{1}{{3}^{{x}_{0}}}$>1 | B. | ?x0∈R,3x0+$\frac{1}{{3}^{{x}_{0}}}$≥1 | ||
| C. | ?x∈R,3x+$\frac{1}{{3}^{{x}$>1 | D. | ?x∈R,3x+$\frac{1}{{3}^{{x}$<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 已知长方体ABCD-A1B1C1D1,P为棱A1B1上一点,BC=10,CD=10,CC1=4,则AP+PC1的最小值为$2\sqrt{74}$.
已知长方体ABCD-A1B1C1D1,P为棱A1B1上一点,BC=10,CD=10,CC1=4,则AP+PC1的最小值为$2\sqrt{74}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com