
分析:本题考查复平面上点的轨迹方程.因为在复平面内点A的坐标为(1,0),l过点A且平行于虚轴,所以直线l上的点对应的复数z的实部为1,可设为z=1+bi(b∈R),然后再求![]() 所对应的点的集合.
所对应的点的集合.
解:如图.因为点A对应的复数为1,直线l过点A且平行于虚轴,所以可设直线l上的点对应的复数为z=1+bi(b∈R).
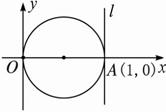
因此![]()
设![]() =x+yi(x、y∈R),
=x+yi(x、y∈R),
于是x+yi=![]()
根据复数相等的条件,有
消去b,有x2+y2=![]()
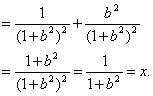
所以x2+y2=x(x≠0),
即(x-![]() )2+y2=
)2+y2=![]() (x≠0).
(x≠0).
所以![]() 所对应的点的集合是以(
所对应的点的集合是以(![]() ,0)为圆心,
,0)为圆心,![]() 为半径的圆,但不包括原点O(0,0).
为半径的圆,但不包括原点O(0,0).
点评 一般说来,求哪个动点的轨迹方程就设哪个动点的坐标为(x,y).所谓动点的轨迹方程就是动点坐标(x,y)所满足的等量关系.常见求曲线方程的方法有:轨迹法、待定系数法、代入法、参数法等.若把参数方程中的参数消去,就可把参数方程转化成普通方程.无论用什么方法求得曲线的方程,都要注意检验以方程的解为坐标的点是否都在曲线上.对此,常从以下两个方面入手:一是看对方程的化简是否采用了非同解变形的手法;二是看是否符合题目的实际意义.其中,用参数法求得的曲线方程中的x、y的范围可由参数函数的值域来确定.


科目:高中数学 来源:学习周报 数学 北师大课标高二版(选修1-2) 2009-2010学年 第36期 总第192期 北师大课标 题型:044
复平面内点A对应的复数为1,过点A作虚轴的平行线l,设l上的点对应的复数为z,试求复数![]() 对应的点集是什么图形?
对应的点集是什么图形?
查看答案和解析>>
科目:高中数学 来源:学习周报 数学 北师大课标高二版(选修2-2) 2009-2010学年 第37期 总第193期 北师大课标 题型:044
复平面内点A对应的复数为1,过点A作虚轴的平行线l,设l上的点对应的复数为z,试求复数![]() 对应的点集是什么图形?
对应的点集是什么图形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com