
某公司生产甲、乙两种桶装产品.已知生产甲产品1桶需耗A原料1千克、B原料2千克;生产乙产品1桶需耗A原料2千克,B原料1千克.每桶甲产品的利润是300元,每桶乙产品的利润是400元.公司在生产这两种产品的计划中,要求每天消耗A、B原料都不超过12千克.求该公司从每天生产的甲、乙两种产品中,可获得的最大利润.
科目:高中数学 来源: 题型:解答题
某企业生产A,B两种产品,生产每吨产品所需的劳动力和煤、电耗如下表: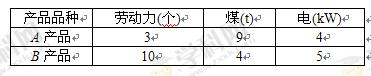
已知生产每吨A产品的利润是5万元,生产每吨B产品的利润是10万元,现因条件限制,该企业仅有劳动力300个,煤360 t,并且供电局只能供电200 kW,试问该企业生产A,B两种产品各多少吨,才能获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知关于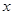 的二次函数
的二次函数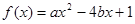 .
.
(1)设集合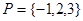 和
和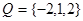 ,分别从集合P和Q中随机取一个数作为
,分别从集合P和Q中随机取一个数作为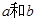 ,求函数
,求函数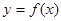 在区间
在区间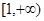 上是增函数的概率;
上是增函数的概率;
(2)设点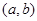 是区域
是区域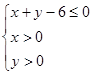 内的随机点,求函数
内的随机点,求函数 在区间
在区间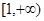 上是增函数的概率.
上是增函数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设x,y满足约束条件 ,
,
(1)画出不等式表示的平面区域,并求该平面区域的面积;
(2)若目标函数z=ax+by(a>0,b>0)的最大值为4,求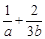 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
已知a+b>0,b<0,那么a,b,-a,-b的大小关系是( )
| A.a>b>-b>-a | B.a>-b>-a>b |
| C.a>-b>b>-a | D.a>b>-a>-b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com