
分析 (1)由条件利用两角和差的正弦公式,化简函数的解析式,再利用正弦函数的单调性求得f(x)的单调递增区间.
(2)根据函数f(x)的解析式,再根据正弦函数的最值,求得函数f(x)的最大值及f(x)取最大值时x的集合.
解答 解:(1)函数f(x)=2sinx•cosx+2cos2x-1=sin2x+cos2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$),
令2kπ-$\frac{π}{2}$≤2x+$\frac{π}{4}$≤2kπ+$\frac{π}{2}$,求得kπ-$\frac{3π}{8}$≤x≤kπ+$\frac{π}{8}$,可得函数的单调增区间为[kπ-$\frac{3π}{8}$,kπ+$\frac{π}{8}$],k∈Z.
(2)由f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),可得当2x+$\frac{π}{4}$=2kπ+$\frac{π}{2}$,k∈Z时,函数f(x)取得最大值为$\sqrt{2}$,
此时,x取值的集合为{x|x=kπ+$\frac{π}{8}$,k∈Z}.
点评 本题主要考查两角和差的正弦公式,正弦函数的单调性和最值,属于基础题.


 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:选择题

| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
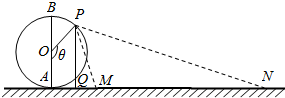 如图,摩天轮的半径OA为50m,它的最低点A距地面的高度忽略不计.地面上有一长度为240m的景观带MN,它与摩天轮在同一竖直平面内,且AM=60m.点P从最低点A处按逆时针方向转动到最高点B处,记∠AOP=θ,θ∈(0,π).
如图,摩天轮的半径OA为50m,它的最低点A距地面的高度忽略不计.地面上有一长度为240m的景观带MN,它与摩天轮在同一竖直平面内,且AM=60m.点P从最低点A处按逆时针方向转动到最高点B处,记∠AOP=θ,θ∈(0,π).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ② | B. | ④ | C. | ①④ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com