某广告公司设计一个凸八边形的商标，它的中间是一个正方形，外面是四个腰长为
，顶角为
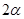的等腰三角形.
（1）若角
时，求该八边形的面积；
（2）写出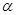
的取值范围，当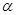取何值时该八边形的面积最大，并求出最大面积.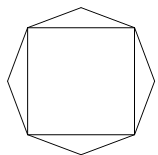
学练快车道快乐假期暑假作业新疆人民出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案科目：高中数学 来源： 题型：解答题
已知函数f(x)＝Asin(2x＋θ)，其中A≠0，θ∈(0，
)．
(1)若函数f(x)的图象过点E(－
，1)，F(
，
)，求函数f(x)的解析式；
(2)如图，点M，N是函数y＝f(x)的图象在y轴两侧与x轴的两个相邻交点，函数图象上一点P(t，
)满足
·
＝
，求函数f(x)的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
如图，在平面直角坐标系中，角
和角
的终边分别与单位圆交于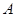
，
两点，（其中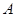为第一象限点，为第二象限点）
（1）若点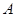的横坐标是
，点的纵坐标是
，求
的值；
（2）若
， 求
的值．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数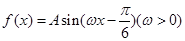
相邻两个对称轴之间的距离是
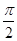，且满足，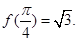
（1）求
的单调递减区间；
（2）在钝角△ABC中，a、b、c分别为角A、B、C的对边，sinB=
,求△ABC的面积。
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
已知函数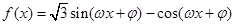
（
，
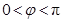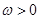）为偶函数，且函数
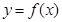图象的两相邻对称轴间的距离为
．
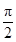(1)求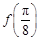
的值；
(2)将函数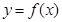的图象向右平移
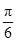个单位后，再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到函数
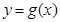的图象，求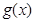
的单调递减区间．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
；（2）
，当
时，八边形的面积取最大值
.
得到角
的最大值.
，
；
，所以
，
，
，
，故
， 
，此时
的值；
时，求函数
的值域.
中，点
，
，其中
.
时，求向量
的坐标；
时，求
的最大值.
的部分图象如图所示.
的解析式，并写出
的内角分别是A，B，C，若
的值.
，
，函数
．
时，求函数
的取值范围；
，且
时，求
的值．