
【题目】如图,在四棱锥P﹣ABCD中,AB∥CD,且∠BAP=∠CDP=90°.(12分) 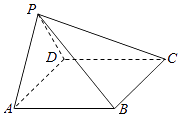
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,∠APD=90°,求二面角A﹣PB﹣C的余弦值.
【答案】
(1)证明:∵∠BAP=∠CDP=90°,∴PA⊥AB,PD⊥CD,
∵AB∥CD,∴AB⊥PD,
又∵PA∩PD=P,且PA平面PAD,PD平面PAD,
∴AB⊥平面PAD,又AB平面PAB,
∴平面PAB⊥平面PAD;
(2)解:∵AB∥CD,AB=CD,∴四边形ABCD为平行四边形,
由(1)知AB⊥平面PAD,∴AB⊥AD,则四边形ABCD为矩形,
在△APD中,由PA=PD,∠APD=90°,可得△PAD为等腰直角三角形,
设PA=AB=2a,则AD= ![]() .
.
取AD中点O,BC中点E,连接PO、OE,
以O为坐标原点,分别以OA、OE、OP所在直线为x、y、z轴建立空间直角坐标系,
则:D( ![]() ),B(
),B( ![]() ),P(0,0,
),P(0,0, ![]() ),C(
),C( ![]() ).
).
![]() ,
, ![]() ,
, ![]() .
.
设平面PBC的一个法向量为 ![]() ,
,
由  ,得
,得 ![]() ,取y=1,得
,取y=1,得 ![]() .
.
∵AB⊥平面PAD,AD平面PAD,∴AB⊥AD,
又PD⊥PA,PA∩AB=A,
∴PD⊥平面PAB,则 ![]() 为平面PAB的一个法向量,
为平面PAB的一个法向量, ![]() .
.
∴cos< ![]() >=
>= ![]() =
= ![]() .
.
由图可知,二面角A﹣PB﹣C为钝角,
∴二面角A﹣PB﹣C的余弦值为 ![]() .
.

【解析】(1.)由已知可得PA⊥AB,PD⊥CD,再由AB∥CD,得AB⊥PD,利用线面垂直的判定可得AB⊥平面PAD,进一步得到平面PAB⊥平面PAD; (2.)由已知可得四边形ABCD为平行四边形,由(1)知AB⊥平面PAD,得到AB⊥AD,则四边形ABCD为矩形,设PA=AB=2a,则AD= ![]() .取AD中点O,BC中点E,连接PO、OE,以O为坐标原点,分别以OA、OE、OP所在直线为x、y、z轴建立空间直角坐标系,求出平面PBC的一个法向量,再证明PD⊥平面PAB,得
.取AD中点O,BC中点E,连接PO、OE,以O为坐标原点,分别以OA、OE、OP所在直线为x、y、z轴建立空间直角坐标系,求出平面PBC的一个法向量,再证明PD⊥平面PAB,得 ![]() 为平面PAB的一个法向量,由两法向量所成角的余弦值可得二面角A﹣PB﹣C的余弦值.
为平面PAB的一个法向量,由两法向量所成角的余弦值可得二面角A﹣PB﹣C的余弦值.
【考点精析】根据题目的已知条件,利用平面与平面垂直的判定的相关知识可以得到问题的答案,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥A﹣BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD. 求证:(Ⅰ)EF∥平面ABC;
(Ⅱ)AD⊥AC.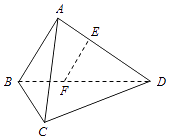
查看答案和解析>>
科目:高中数学 来源: 题型:
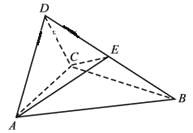
【题目】如图,四面体![]() 中,
中, ![]() 是正三角形,
是正三角形, ![]() 是直角三角形,
是直角三角形, ![]() ,
,![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)过![]() 的平面交
的平面交![]() 于点
于点![]() ,若平面
,若平面![]() 把四面体
把四面体![]() 分成体积相等的两部分,求二面角
分成体积相等的两部分,求二面角![]() 的大小。
的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M过C(1,-1),D(-1,1)两点,且圆心M在x+y-2=0上.
(1)求圆M的方程;
(2)设点P是直线3x+4y+8=0上的动点,PA,PB是圆M的两条切线,A,B为切点,求四边形PAMB面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图程序框图是为了求出满足3n﹣2n>1000的最小偶数n,那么在 ![]() 和
和 ![]() 两个空白框中,可以分别填入( )
两个空白框中,可以分别填入( )
A.A>1000和n=n+1
B.A>1000和n=n+2
C.A≤1000和n=n+1
D.A≤1000和n=n+2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-5:不等式选讲]
已知函数f(x)=﹣x2+ax+4,g(x)=|x+1|+|x﹣1|.(10分)
(1)当a=1时,求不等式f(x)≥g(x)的解集;
(2)若不等式f(x)≥g(x)的解集包含[﹣1,1],求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】棱长为1的正方体![]() 中,
中,![]() 分别是
分别是![]() 的中点.
的中点.
①![]() 在直线
在直线![]() 上运动时,三棱锥
上运动时,三棱锥![]() 体积不变;
体积不变;
②![]() 在直线
在直线![]() 上运动时,
上运动时,![]() 始终与平面
始终与平面![]() 平行;
平行;
③平面![]() 平面
平面![]() ;
;
④连接正方体![]() 的任意的两个顶点形成一条直线,其中与棱
的任意的两个顶点形成一条直线,其中与棱![]() 所在直线异面的有
所在直线异面的有![]() 条;
条;
其中真命题的编号是_______________.(写出所有正确命题的编号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com