
【题目】在四棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
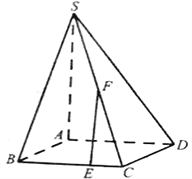
(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)若底面![]() 为矩形,
为矩形,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】
试题(Ⅰ)由题意![]() 平面
平面![]() ,得到所以
,得到所以![]() ,同理可证
,同理可证![]() ,利用线面垂直的判定定理,即可证得
,利用线面垂直的判定定理,即可证得![]() 平面
平面![]() ;
;
(Ⅱ)分别以![]() 、
、![]() 、
、![]() 所在方向为
所在方向为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系![]() ,求得向量
,求得向量![]() 和平面
和平面![]() 的一个法向量为
的一个法向量为![]() ,利用向量的夹角公式,即可求解直线与平面所成的角的正弦值.
,利用向量的夹角公式,即可求解直线与平面所成的角的正弦值.
试题解析:
(Ⅰ)证法1:在平面![]() 内过点
内过点![]() 作两条直线
作两条直线![]() ,
,![]() ,
,
使得![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() ,
,![]() 为两条相交直线.
为两条相交直线.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .所以
.所以![]() .同理可证
.同理可证![]() .又因为
.又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .
.
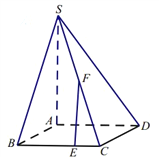
证法2:在平面![]() 内过点
内过点![]() 作
作![]() ,在平面
,在平面![]() 内过点
内过点![]() 作
作![]() .
.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() .同理可证
.同理可证![]() 平面
平面![]() .而过点
.而过点![]() 作平面
作平面![]() 的垂线有且仅有一条,所以
的垂线有且仅有一条,所以![]() 与
与![]() 重合.所以
重合.所以![]() 平面
平面![]() .所以,直线
.所以,直线![]() 为平面
为平面![]() 与平面
与平面![]() 的交线.所以,直线
的交线.所以,直线![]() 与直线
与直线![]() 重合.所以
重合.所以![]() 平面
平面![]() .
.
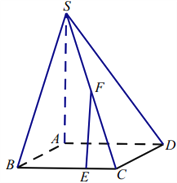
(Ⅱ)如图,分别以![]() 、
、![]() 、
、![]() 所在方向为
所在方向为![]() 轴、
轴、![]() 轴、
轴、![]() 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系![]() .设
.设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
由![]() 为
为![]() 的中点,得
的中点,得![]() ;由
;由![]() ,得
,得![]() .所以
.所以![]() ,
,![]() ,
,![]() .设平面
.设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则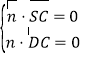 ,即
,即![]() .取
.取![]() ,则
,则![]() ,
,![]() .所以
.所以![]() .
.
所以![]()
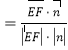
![]() .
.
所以,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】为弘扬中华传统文化,学校课外阅读兴趣小组进行每日一小时的“经典名著”和“古诗词”的阅读活动. 根据调查,小明同学阅读两类读物的阅读量统计如下:
小明阅读“经典名著”的阅读量![]() (单位:字)与时间t(单位:分钟)满足二次函数关系,部分数据如下表所示;
(单位:字)与时间t(单位:分钟)满足二次函数关系,部分数据如下表所示;
t | 0 | 10 | 20 | 30 |
| 0 | 2700 | 5200 | 7500 |
阅读“古诗词”的阅读量![]() (单位:字)与时间t(单位:分钟)满足如图1所示的关系.
(单位:字)与时间t(单位:分钟)满足如图1所示的关系.

(1)请分别写出函数![]() 和
和![]() 的解析式;
的解析式;
(2)在每天的一小时课外阅读活动中,小明如何分配“经典名著”和“古诗词”的阅读时间,使每天的阅读量最大,最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,共享单车已经悄然进入了广大市民的日常生活,并慢慢改变了人们的出行方式.为了更好地服务民众,某共享单车公司在其官方![]() 中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出
中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出![]() 条较为详细的评价信息进行统计,车辆状况的优惠活动评价的
条较为详细的评价信息进行统计,车辆状况的优惠活动评价的![]() 列联表如下:
列联表如下:
对优惠活动好评 | 对优惠活动不满意 | 合计 | |
对车辆状况好评 |
|
|
|
对车辆状况不满意 |
|
|
|
合计 |
|
|
|
(1)能否在犯错误的概率不超过![]() 的前提下认为优惠活动好评与车辆状况好评之间有关系?
的前提下认为优惠活动好评与车辆状况好评之间有关系?
(2)为了回馈用户,公司通过![]() 向用户随机派送骑行券.用户可以将骑行券用于骑行付费,也可以通过
向用户随机派送骑行券.用户可以将骑行券用于骑行付费,也可以通过![]() 转赠给友.某用户共获得了
转赠给友.某用户共获得了![]() 张骑行券,其中只有
张骑行券,其中只有![]() 张是一元券.现该用户从这
张是一元券.现该用户从这![]() 张骑行券中随机选取
张骑行券中随机选取![]() 张转赠给好友,求选取的
张转赠给好友,求选取的![]() 张中至少有
张中至少有![]() 张是一元券的概率.
张是一元券的概率.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
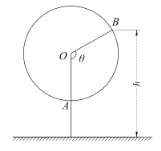
【题目】如图为某儿童游乐场一个小型摩天轮示意图,该摩天轮近似看作半径为![]() 的圆,圆上最低点A与地面距离为
的圆,圆上最低点A与地面距离为![]() ,摩天轮每60秒匀速转动一圈,摩天轮上某点B的起始位置在最低点A处.图中
,摩天轮每60秒匀速转动一圈,摩天轮上某点B的起始位置在最低点A处.图中![]() 与地面垂直,以
与地面垂直,以![]() 为始边,逆时针转动
为始边,逆时针转动![]() 角到
角到![]() ,设B点与地面间的距离为
,设B点与地面间的距离为![]() .
.
(1)求h与![]() 间关系的函数解析式;
间关系的函数解析式;
(2)设从![]() 开始转动,经过t秒后到达
开始转动,经过t秒后到达![]() ,求h与t之间的函数关系式;
,求h与t之间的函数关系式;
(3)如果离地面高度不低于![]() 才能获得最佳观景效果,在摩天轮转动的一圈内,有多长时间B点在最佳观景效果高度?
才能获得最佳观景效果,在摩天轮转动的一圈内,有多长时间B点在最佳观景效果高度?
查看答案和解析>>
科目:高中数学 来源: 题型:
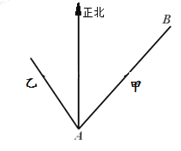
【题目】已知海岛![]() 在海岛
在海岛![]() 北偏东
北偏东![]() ,
,![]() ,
,![]() 相距
相距![]() 海里,物体甲从海岛
海里,物体甲从海岛![]() 以
以![]() 海里/小时的速度沿直线向海岛
海里/小时的速度沿直线向海岛![]() 移动,同时物体乙从海岛
移动,同时物体乙从海岛![]() 沿着海岛
沿着海岛![]() 北偏西
北偏西![]() 方向以
方向以![]() 海里/小时的速度移动.
海里/小时的速度移动.
(1)问经过多长时间,物体甲在物体乙的正东方向;
(2)求甲从海岛![]() 到达海岛
到达海岛![]() 的过程中,甲、乙两物体的最短距离.
的过程中,甲、乙两物体的最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数y=g(x)的图象在![]() 处的切线方程;
处的切线方程;
(2)求y=g(x)的最大值;
(3)令f(x)=ax2+bx﹣x(g(x))(a,b∈R).若a≥0,求f(x)的单调区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com