练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．两动直线3x+2y=6t与3tx-2ty=6相交于P，若取t为参数，求P点轨迹方程．

    分析 两动直线3x+2y=6t与3tx-2ty=6，联立成方程组，可得x=t+$\frac{1}{t}$，y=$\frac{3}{2}$（t-$\frac{1}{t}$），即可求P点轨迹方程．

    解答 解：两动直线3x+2y=6t与3tx-2ty=6，联立成方程组，可得x=t+$\frac{1}{t}$，y=$\frac{3}{2}$（t-$\frac{1}{t}$），
    ∴P点轨迹方程是$\left\{\begin{array}{l}{x=t+\frac{1}{t}}\\{y=\frac{3}{2}（t-\frac{1}{t}）}\end{array}\right.$（t为参数）．

    点评 本题考查求P点轨迹方程，考查参数法的运用，正确解方程组是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    14．函数f（x）=4x-2x+1的最小值为-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．当m取不同的有理数时，讨论幂函数y=xm的定义域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．不等式|1-3x|≤2的解集为（　　）
    A．（-∞，-1]B．[-$\frac{1}{3}$，+∞）C．[-$\frac{1}{3}$，1]D．[-1，$\frac{1}{3}$]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

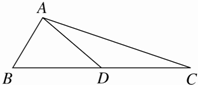    19．如图，在△ABC中，BC边上的中线AD长为3，且sinB=$\frac{\sqrt{10}}{8}$，cos∠ADC=-$\frac{1}{4}$．
    （Ⅰ）求sin∠BAD的值；
    （Ⅱ）求AC边的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．若集合A={x|y=$\sqrt{x-3}$}，B={y|y=x2+2}，则A∩B等于（　　）
    A．[3，+∞）B．（3，+∞）C．[2，+∞）D．（0，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．若满足c=2，面积S=$\frac{1}{2}$$\overrightarrow{CA}$•$\overrightarrow{CB}$的△ABC有两个，则边长BC的取值范围是（2，2$\sqrt{2}$）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

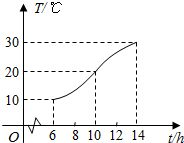    17．如图，某地一天中6时至14时的温度变化曲线近似满足函数y=Asin（ωx+φ）+b（其中$\frac{π}{2}＜φ＜π$），与图中曲线对应的函数解析式是$y=10sin（\frac{π}{8}x+\frac{3π}{4}）+20，x∈[{6，14}]$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知复数z满足（1-i）z=3+5i，则复数z在复平面内对应的点位于（　　）
    A．第一象限B．第二象限C．第三象限D．第四象限

    查看答案和解析>>

    同步练习册答案