
”¾ĢāÄæ”æÓŠŅ»Ī»Ķ¬Ń§¼ŅĄļæŖĮĖŅ»øöŠ”Āō²æ,ĖūĪŖĮĖŃŠ¾æĘųĪĀ¶ŌČČ²čĻśŹŪµÄÓ°Ļģ,¾¹żĶ³¼Ę,µĆµ½Ņ»øöĀō³öČČ²č±ŹżÓėµ±ĢģĘųĪĀµÄ¶Ō±Č±ķČēĻĀ:
ĘųĪĀx/”ę | -5 | 0 | 4 | 7 | 12 | 15 | 19 | 23 | 27 | 31 | 36 |
ČČ²čĻśŹŪ±Źży/± | 156 | 150 | 132 | 128 | 130 | 116 | 104 | 89 | 93 | 76 | 54 |
(1)»³öÉ¢µćĶ¼;
(2)ÄćÄÜ“ÓÉ¢µćĶ¼ÖŠ·¢ĻÖĘųĪĀÓėČČ²čµÄĻśŹŪ±ŹżÖ®¼ä¹ŲĻµµÄŅ»°ć¹ęĀÉĀš?
(3)Čē¹ū½üĖĘ³ÉĻߊŌ¹ŲĻµµÄ»°,Ēė»³öŅ»ĢõÖ±Ļߥ“½üĖʵŲ±ķŹ¾ÕāÖÖĻߊŌ¹ŲĻµ;
(4)ŹŌĒó³ö»Ų¹éÖ±Ļß·½³Ģ;
(5)ĄūÓĆ(4)µÄ»Ų¹é·½³Ģ,ČōijĢģµÄĘųĪĀŹĒ2 ”ę,Ō¤²āÕāŅ»ĢģĀō³öČČ²čµÄ±Źż.
”¾“š°ø”æ£Ø1£©¼ū½āĪö£»£Ø2£©¼ū½āĪö£»£Ø3£©¼ū½āĪö£»£Ø4£©![]() £»£Ø5£©143
£»£Ø5£©143
”¾½āĪö”æ·ÖĪö£ŗ£Ø1£©ŅŌxÖį±ķŹ¾ĘųĪĀ,ŅŌyÖį±ķŹ¾ČČ²č±Źż,æÉ×÷É¢µćĶ¼£»
£Ø2£©“ÓĶ¼ÖŠæÉŅŌ擳ö,ø÷µćÉ¢²¼ŌŚ“Ó×óÉĻ½Ēµ½ÓŅĻĀ½ĒµÄĒųÓņĄļ,Ņņ“ĖČČ²čµÄĻśŹŪ±ŹżÓėĘųĪĀŹĒĻą¹ŲµÄ,ĘųĪĀŌ½øß,Āō³öČ„µÄČČ²č±ŹżŌ½ÉŁ£»
£Ø3£©“ÓÉ¢µćĶ¼æÉŅŌ擳ö,ÕāŠ©µć“óÖĀ·Ö²¼ŌŚŅ»ĢõÖ±Ļßø½½ü,øł¾Ż²»Ķ¬µÄ±ź×¼æÉŅŌ»³ö²»Ķ¬µÄÖ±Ļߥ“½üĖʵŲ±ķŹ¾ÕāÖÖĻߊŌĻą¹Ų¹ŲĻµ£»
£Ø4£©ÓÉĢāÖŠĖłøųµÄŹż¾ŻĒóµĆ»Ų¹é·½³Ģ¼“æÉ£»
£Ø5£©½įŗĻ»Ų¹é·½³ĢµÄŌ¤²ā×÷ÓĆŗĶ£Ø4£©ÖŠµÄ½įĀŪÕūĄķ¼ĘĖć¼“æÉĒóµĆ×īÖÕ½į¹ū.
Ļź½ā£ŗ(1)ŅŌxÖį±ķŹ¾ĘųĪĀ,ŅŌyÖį±ķŹ¾ČČ²č±Źż,æÉ×÷É¢µćĶ¼ČēĻĀĶ¼ĖłŹ¾.
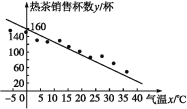
(2)“ÓĶ¼ÖŠæÉŅŌ擳ö,ø÷µćÉ¢²¼ŌŚ“Ó×óÉĻ½Ēµ½ÓŅĻĀ½ĒµÄĒųÓņĄļ,Ņņ“ĖČČ²čµÄĻśŹŪ±ŹżÓėĘųĪĀŹĒĻą¹ŲµÄ,ĘųĪĀŌ½øß,Āō³öČ„µÄČČ²č±ŹżŌ½ÉŁ.
(3)“ÓÉ¢µćĶ¼æÉŅŌ擳ö,ÕāŠ©µć“óÖĀ·Ö²¼ŌŚŅ»ĢõÖ±Ļßø½½ü,øł¾Ż²»Ķ¬µÄ±ź×¼æÉŅŌ»³ö²»Ķ¬µÄÖ±Ļߥ“½üĖʵŲ±ķŹ¾ÕāÖÖĻߊŌĻą¹Ų¹ŲĻµ,ČēĶ¼ĖłŹ¾.
(4)Ņņ![]() 335,
335,![]() 778.
778.
Ėł ”Ö-2.35,
”Ö-2.35,
![]()
ĖłŅŌ»Ų¹éÖ±Ļß·½³Ģ![]()
(5)ÓÉ(4)µÄ·½³Ģ,µ±x=2![]() 2 ”ę,ÕāŅ»Ģģ“óŌ¼æÉŅŌĀō³ö143±ČČ²č.
2 ”ę,ÕāŅ»Ģģ“óŌ¼æÉŅŌĀō³ö143±ČČ²č.


 ¼ĘĖćøߏÖĻµĮŠ“š°ø
¼ĘĖćøߏÖĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖČżĄā׶P£ABCµÄĖÄøö¶„µćŌŚĒņOµÄĒņĆęÉĻ£¬PA=PB=PC£¬”÷ABCŹĒ±ß³¤ĪŖ![]() µÄÕżČż½ĒŠĪ£¬E£¬F·Ö±šŹĒPA£¬ABµÄÖŠµć£¬”ĻCEF=90”ć.ŌņĒņOµÄĢå»żĪŖ£Ø £©
µÄÕżČż½ĒŠĪ£¬E£¬F·Ö±šŹĒPA£¬ABµÄÖŠµć£¬”ĻCEF=90”ć.ŌņĒņOµÄĢå»żĪŖ£Ø £©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŗÆŹżf(x)=![]() +bx+c,
+bx+c,
(1)Čōf(x)ŌŚ(-”Ž,+”Ž)ÉĻŹĒŌöŗÆŹż,ĒóbµÄȔֵ·¶Ī§;
(2)Čōf(x)ŌŚx=1“¦Č”µĆ¼«Öµ,ĒŅx”Ź[-1,2]Ź±,f(x)<c2ŗć³ÉĮ¢,ĒócµÄȔֵ·¶Ī§.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÉčf£Øx£©ŹĒ¶ØŅåŌŚRÉĻĒŅÖÜĘŚĪŖ2µÄŗÆŹż£¬ŌŚĒų¼ä[©1£¬1]ÉĻ£¬f£Øx£©= 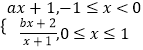 ĘäÖŠa£¬b”ŹR£®Čō
ĘäÖŠa£¬b”ŹR£®Čō ![]() =
= ![]() £¬Ōņa+3bµÄÖµĪŖ £®
£¬Ōņa+3bµÄÖµĪŖ £®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijµŲĒų2010ÄźÖĮ2016ÄźÅ©“å¾ÓĆń¼ŅĶ„ČĖ¾ł“æŹÕČėy(µ„Ī»:Ē§ŌŖ)µÄŹż¾ŻČēĻĀ±ķ:
Äź””·Ż | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
Äź·Ż“śŗÅt | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
ČĖ¾ł“æŹÕČėy | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)Ēóy¹ŲÓŚtµÄ»Ų¹éÖ±Ļß·½³Ģ;
(2)ĄūÓĆ(1)ÖŠµÄ»Ų¹é·½³Ģ,·ÖĪö2010ÄźÖĮ2016ÄźøƵŲĒųÅ©“å¾ÓĆń¼ŅĶ„ČĖ¾ł“æŹÕČėµÄ±ä»ÆĒéæö,²¢Ō¤²āøƵŲĒų2018ÄźÅ©“å¾ÓĆń¼ŅĶ„ČĖ¾ł“æŹÕČė.
ø½:»Ų¹éÖ±ĻߵĊ±ĀŹŗĶ½Ų¾ąµÄ×īŠ”¶ž³Ė¹Ą¼Ę¹«Ź½·Ö±š
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠĖµ·Ø£ŗ
¢Ł½«Ņ»×鏿¾ŻÖŠµÄĆæøöŹż¾Ż¶¼¼ÓÉĻ»ņ¼õČ„Ķ¬Ņ»øö³£Źżŗ󣬷½²īŗć²»±ä£»
¢ŚÉčÓŠŅ»øö»Ų¹é·½³Ģ![]() £¬Čō±äĮæ
£¬Čō±äĮæ![]() Ōö¼ÓŅ»øöµ„Ī»Ź±£¬Ōņ
Ōö¼ÓŅ»øöµ„Ī»Ź±£¬Ōņ![]() Ę½¾łŌö¼Ó5øöµ„Ī»£»
Ę½¾łŌö¼Ó5øöµ„Ī»£»
¢ŪĻߊŌ»Ų¹é·½³Ģ![]() ĖłŌŚÖ±Ļß±Ų¹ż
ĖłŌŚÖ±Ļß±Ų¹ż![]() £»
£»
¢ÜĒśĻßÉĻµÄµćÓėøƵćµÄ×ų±źÖ®¼ä¾ßÓŠĻą¹Ų¹ŲĻµ£»
¢ŻŌŚŅ»øö![]() ĮŠĮŖ±ķÖŠ£¬ÓɼĘĖćµĆ
ĮŠĮŖ±ķÖŠ£¬ÓɼĘĖćµĆ![]() £¬ŌņĘäĮ½øö±äĮæÖ®¼äÓŠ¹ŲĻµµÄæÉÄÜŠŌŹĒ
£¬ŌņĘäĮ½øö±äĮæÖ®¼äÓŠ¹ŲĻµµÄæÉÄÜŠŌŹĒ![]() .
.
ĘäÖŠ“ķĪóµÄŹĒ________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»øöÉĢ³”¾ĻśÄ³ÖÖÉĢĘ·£¬øł¾ŻŅŌĶł×ŹĮĻĶ³¼Ę£¬ĆæĪ»¹ĖæĶ²ÉÓƵķÖĘŚø¶æī“ĪŹż![]() µÄ·Ö²¼ĮŠĪŖ£ŗ
µÄ·Ö²¼ĮŠĪŖ£ŗ
| 1 | 2 | 3 | 4 | 5 |
| 0.4 | 0.2 | 0.2 | 0.1 | 0.1 |
ÉĢ³”¾ĻśŅ»¼žøĆÉĢĘ·£¬²ÉÓĆ1ĘŚø¶æī£¬ĘäĄūČóĪŖ200ŌŖ£»²ÉÓĆ2ĘŚ»ņ3ĘŚø¶æī£¬ĘäĄūČóĪŖ250ŌŖ£»²ÉÓĆ4ĘŚ»ņ5ĘŚø¶æī£¬ĘäĄūČóĪŖ300ŌŖ£®![]() ±ķŹ¾¾ĻśŅ»¼žøĆÉĢĘ·µÄĄūČó£®
±ķŹ¾¾ĻśŅ»¼žøĆÉĢĘ·µÄĄūČó£®
(1)Ēó¹ŗĀņøĆÉĢĘ·µÄ3Ī»¹ĖæĶÖŠ£¬Ē”ÓŠ2Ī»²ÉÓĆ1ĘŚø¶æīµÄøÅĀŹ£»
(2)Ēó![]() µÄ·Ö²¼ĮŠ¼°ĘŚĶū
µÄ·Ö²¼ĮŠ¼°ĘŚĶū![]() £®
£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬Ļ߶Ī![]() µÄ³¤¶ČĪŖ
µÄ³¤¶ČĪŖ![]() £¬ŌŚĻ߶Ī
£¬ŌŚĻ߶Ī![]() ÉĻČ”Į½øöµć
ÉĻČ”Į½øöµć![]() £¬Ź¹µĆ
£¬Ź¹µĆ![]() £¬ŅŌ
£¬ŅŌ![]() ĪŖŅ»±ßŌŚĻ߶Ī
ĪŖŅ»±ßŌŚĻ߶Ī![]() µÄÉĻ·½×öŅ»øöÕżĮł±ßŠĪ£¬Č»ŗóČ„µōĻ߶Ī
µÄÉĻ·½×öŅ»øöÕżĮł±ßŠĪ£¬Č»ŗóČ„µōĻ߶Ī![]() £¬µĆµ½Ķ¼2ÖŠµÄĶ¼ŠĪ£»¶ŌĶ¼2ÖŠµÄ×īÉĻ·½µÄĻ߶Ī
£¬µĆµ½Ķ¼2ÖŠµÄĶ¼ŠĪ£»¶ŌĶ¼2ÖŠµÄ×īÉĻ·½µÄĻ߶Ī![]() ×÷ĻąĶ¬µÄ²Ł×÷£¬µĆµ½Ķ¼3ÖŠµÄĶ¼ŠĪ£»ŅĄ“ĖĄąĶĘ£¬ĪŅĆĒ¾ĶµĆµ½ĮĖŅŌĻĀŅ»ĻµĮŠĶ¼ŠĪ£ŗ
×÷ĻąĶ¬µÄ²Ł×÷£¬µĆµ½Ķ¼3ÖŠµÄĶ¼ŠĪ£»ŅĄ“ĖĄąĶĘ£¬ĪŅĆĒ¾ĶµĆµ½ĮĖŅŌĻĀŅ»ĻµĮŠĶ¼ŠĪ£ŗ

¼ĒµŚ![]() øöĶ¼ŠĪ£ØĶ¼1ĪŖµŚ1øöĶ¼ŠĪ£©ÖŠµÄĖłÓŠĻ߶Ī³¤µÄŗĶĪŖ
øöĶ¼ŠĪ£ØĶ¼1ĪŖµŚ1øöĶ¼ŠĪ£©ÖŠµÄĖłÓŠĻ߶Ī³¤µÄŗĶĪŖ![]() £¬ĻÖøų³öÓŠ¹ŲŹżĮŠ
£¬ĻÖøų³öÓŠ¹ŲŹżĮŠ![]() µÄĖÄøöĆüĢā£ŗ
µÄĖÄøöĆüĢā£ŗ
¢ŁŹżĮŠ![]() ŹĒµČ±ČŌŽĮŠ£»
ŹĒµČ±ČŌŽĮŠ£»
¢ŚŹżĮŠ![]() ŹĒµŻŌöŹżĮŠ£»
ŹĒµŻŌöŹżĮŠ£»
¢Ū“ęŌŚ×īŠ”µÄÕżŹż![]() £¬Ź¹µĆ¶ŌČĪŅāµÄÕżÕūŹż
£¬Ź¹µĆ¶ŌČĪŅāµÄÕżÕūŹż![]() £¬¶¼ÓŠ
£¬¶¼ÓŠ![]() £»
£»
¢Ü“ęŌŚ×ī“óµÄÕżŹż![]() £¬Ź¹µĆ¶ŌČĪŅāµÄÕżÕūŹż
£¬Ź¹µĆ¶ŌČĪŅāµÄÕżÕūŹż![]() £¬¶¼ÓŠ
£¬¶¼ÓŠ![]() .
.
ĘäÖŠÕęĆüĢāµÄŠņŗÅŹĒ__________£® (ĒėŠ“³öĖłÓŠÕęĆüĢāµÄŠņŗÅ£©.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪåøöČĖÕ¾³ÉŅ»ÅÅ£¬ĒóŌŚĻĀĮŠĢõ¼žĻĀµÄ²»Ķ¬ÅÅ·ØÖÖŹż£ŗ
£Ø1£©¼×±ŲŠėŌŚÅÅĶ·£»
£Ø2£©¼×”¢ŅŅĻąĮŚ£»
£Ø3£©¼×²»ŌŚÅÅĶ·£¬²¢ĒŅŅŅ²»ŌŚÅÅĪ²£»
£Ø4£©ĘäÖŠ¼×”¢ŅŅĮ½ČĖ×Ō×óĻņÓŅ“Óøßµ½°«ÅÅĮŠĒŅ»„²»ĻąĮŚ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com