[题目]已知函数是定义在实数集R上的奇函数.且在区间上是单调递增.若.则的取值范围为．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知函数是定义在实数集R上的奇函数，且在区间上是单调递增，若，则的取值范围为_______．

【答案】

【解析】

先将函数中的变量化简，再确定函数f（x）是在实数集R上单调递增，利用函数的单调性，即可求得x的取值范围．

∵lg2lg50+（lg5）2=（1﹣lg5）（1+lg5）+（lg5）2=1

∴f（lg2lg50+（lg5）2）+f（lgx﹣2）＜0，可化为f（1）+f（lgx﹣2）＜0，

∵函数f（x）是定义在实数集R上的奇函数，

∴f（lgx﹣2）＜f（﹣1）

∵函数f（x）是定义在实数集R上的奇函数，且在区间[0，+∞）上是单调递增，

∴函数f（x）是在实数集R上单调递增

∴lgx﹣2＜﹣1

∴lgx＜1

∴0＜x＜10

故答案为：（0，10）．

练习册系列答案

花山小状元学科能力达标初中生100全优卷系列答案

金考卷百校联盟高考考试大纲调研卷系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】某旅游区每年各个月份接待游客的人数近似地满足周期性规律，因而，第个月从事旅游服务工作的人数可近似地用函数来刻画，其中，正整数表示月份，为正整数，.

统计发现，该地区每年各个月份从事旅游服务工作的人数有以下规律：

（i）每年相同的月份，该地区从事旅游服务工作的人数基本相同；

（ii）该地区从事旅游服务工作的人数最多的8月份和最少的2月份相差约400人；

（iii）2月份该地区从事旅游服务工作的人数约为100人，随后逐月递增直到8月份达到最多.

（1）根据已知信息，试确定一个符合条件的的表达式.

（2）一般地，当该地区从事旅游服务工作的人数在400或400以上时，该地区也进入了一年中的旅游“旺季”.求一年中的哪几个月是该地区的旅游旺季？请说明理由.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设{an}和{bn}是两个等差数列,记cn=max{b1-a1n,b2-a2n,…,bn-ann}(n=1,2,3,…),其中max{x1,x2,…,xs}表示x1,x2,…,xs这s个数中最大的数.

(Ⅰ)若an=n,bn=2n-1,求c1,c2,c3的值,并证明{cn}是等差数列;

(Ⅱ)证明:或者对任意正数M,存在正整数m,当n≥m时, >M;或者存在正整数m,使得cm,cm+1,cm+2,…是等差数列.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】点为圆上一动点，轴于点，记线段的中点的运动轨迹为曲线.

（1）求曲线的方程；

（2）直线经过定点，且与曲线交于两点，求面积的最大值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】从全校参加科技知识竞赛初赛的学生试卷中，抽取一个样本，考察竞赛的成绩分布.将样本分成5组，绘成频率分布直方图（如图），图中从左到右各小组的小长方形的高之比是，最后一组的频数是6.请结合频率分布直方图提供的信息，解答下列问题：

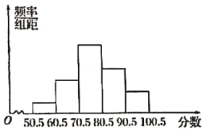
（1）样本的容量是多少?

（2）求样本中成绩在分的学生人数；

（3）从样本中成绩在90.5分以上的同学中随机地抽取2人参加决赛，求最高分甲被抽到的概率.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，，，是同一平面内的三条平行直线，与之间的距离是1，与之间的距离是2，三角形的三个顶点分别在，，上.

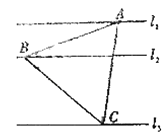
（1）若为正三角形，求其边长；

（2）若是以B为直角顶点的直角三角形，求其面积的最小值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知的一个顶点为抛物线的顶点，，两点都在抛物线上，且.

（1）求证：直线必过一定点；

（2）求证：面积的最小值.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图所示，某街道居委会拟在地段的居民楼正南方向的空白地段上建一个活动中心，其中米．活动中心东西走向，与居民楼平行. 从东向西看活动中心的截面图的下部分是长方形，上部分是以为直径的半圆. 为了保证居民楼住户的采光要求，活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长不超过米，其中该太阳光线与水平线的夹角满足.