
【题目】已知椭圆C的方程为 ![]() +
+ ![]() =1(a>b>0),双曲线
=1(a>b>0),双曲线 ![]() ﹣
﹣ ![]() =1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4
=1的一条渐近线与x轴所成的夹角为30°,且双曲线的焦距为4 ![]() .
.
(1)求椭圆C的方程;
(2)设F1 , F2分别为椭圆C的左,右焦点,过F2作直线l(与x轴不重合)交于椭圆于A,B两点,线段AB的中点为E,记直线F1E的斜率为k,求k的取值范围.
【答案】
(1)解:由一条渐近线与x轴所成的夹角为30°,则 ![]() =tan30°=
=tan30°= ![]() ,即a2=3b2,
,即a2=3b2,
由2c=4 ![]() .c=2
.c=2 ![]() ,则a2+b2=8,
,则a2+b2=8,
解得:a2=8,b2=2,
∴椭圆的标准方程: ![]()
(2)解:由(1)可知:F2(2,0),直线AB的方程:x=ty+2,A(x1,y1),B(x2,y2),
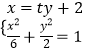 ,整理得:(t2+3)y2+4ty﹣2=0,
,整理得:(t2+3)y2+4ty﹣2=0,
y1+y2=﹣ ![]() ,x1+x2=
,x1+x2= ![]() ,
,
则E( ![]() ,﹣
,﹣ ![]() ),
),
由F1(﹣2,0),则直线F1E的斜率k= 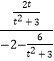 =﹣
=﹣ ![]() ,
,
①当t=0时,k=0,
②当t≠0时,丨k丨= ![]() =
= ![]() ≤
≤ ![]() ,
,
即丨k丨∈(0, ![]() ],
],
∴k的取值范围[﹣ ![]() ,
, ![]() ]
]
【解析】(1)由双曲线的渐近线方程及斜率公式,即可求得a2=3b2,c=2 ![]() ,即a2+b2=8,即可求得a和b的值,求得椭圆方程;(2)设直线AB的方程,代入椭圆方程,利用韦达定理求得斜率丨k丨用t表示,利用基本不等式即可求得k的取值范围.
,即a2+b2=8,即可求得a和b的值,求得椭圆方程;(2)设直线AB的方程,代入椭圆方程,利用韦达定理求得斜率丨k丨用t表示,利用基本不等式即可求得k的取值范围.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】水培植物需要一种植物专用营养液,已知每投放![]() (
(![]() 且
且![]() )个单位的营养液,它在水中释放的浓度
)个单位的营养液,它在水中释放的浓度![]() (克/升)随着时间
(克/升)随着时间![]() (天)变化的函数关系式近似为
(天)变化的函数关系式近似为![]() ,其中
,其中 ,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
,若多次投放,则某一时刻水中的营养液浓度为每次投放的营养液在相应时刻所释放的浓度之和,根据经验,当水中营养液的浓度不低于4(克/升)时,它才能有效.
(1)若只投放一次2个单位的营养液,则有效时间最多可能达到几天?
(2)若先投放2个单位的营养液,3天后再投放![]() 个单位的营养液,要使接下来的2天中,营养液能够持续有效,试求
个单位的营养液,要使接下来的2天中,营养液能够持续有效,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]()
(Ⅰ)求函数![]() 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(Ⅱ)当![]() 时,方程
时,方程![]() 恰有两个不同的实数根,求实数
恰有两个不同的实数根,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)将函数![]() 的图象向右平移
的图象向右平移![]() (
(![]() )个单位后所得函数
)个单位后所得函数![]() 的图象关于原点中心对称,求
的图象关于原点中心对称,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
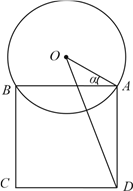
【题目】某校一个校园景观的主题为“托起明天的太阳”,其主体是一个半径为5米的球体,需设计一个透明的支撑物将其托起,该支撑物为等边圆柱形的侧面,厚度忽略不计.轴截面如图所示,设![]() .(注:底面直径和高相等的圆柱叫做等边圆柱.)
.(注:底面直径和高相等的圆柱叫做等边圆柱.)
(1)用![]() 表示圆柱的高;
表示圆柱的高;
(2)实践表明,当球心![]() 和圆柱底面圆周上的点
和圆柱底面圆周上的点![]() 的距离达到最大时,景观的观赏效
的距离达到最大时,景观的观赏效
果最佳,求此时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 有如下性质:该函数在
有如下性质:该函数在![]() 上是减函数,在
上是减函数,在![]() 上是增函数.
上是增函数.
(1)已知![]() ,利用上述性质,求函数
,利用上述性质,求函数![]() 的单调区间和值域;
的单调区间和值域;
(2)对于(1)中的函数![]() 和函数
和函数![]() ,若对任意
,若对任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图四边形ABCD为边长为2的菱形,G为AC与BD交点,平面BED⊥平面ABCD,BE=2,AE=2 ![]() .
. 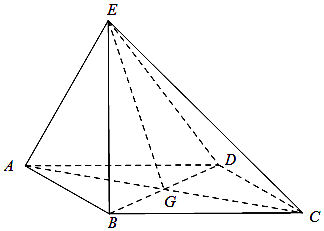
(Ⅰ)证明:BE⊥平面ABCD;
(Ⅱ)若∠ABC=120°,求直线EG与平面EDC所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com