练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知数列中， .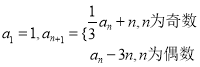

    （1）求证：数列是等比数列；

    （2）若是数列的前项和，求满足的所有正整数.

    【答案】（1）见解析；（2）1和2．

    【解析】试题分析：（1）要证明数列是等比数列，只需根据等比数列的定义，为此设，因此证明为常数即可；（2）首先要求的通项，由（1）可得出，即，则递推式可得，由于通项要分类，因此求数列的和时，我们也分类讲解， ，

    ，这是递减的，计算发现，又，同理可得，即满足题意的只有1和2两个数．

    试题解析：（Ⅰ）设，

    因为

    ==,

    所以数列是以即为首项，以为公比的等比数列． 5分

    （Ⅱ）由（Ⅰ）得，即，

    由，得，

    所以，

    ．10分

    显然当时， 单调递减，

    又当时， ＞0，当时， ＜0，所以当时， ＜0；

    ，

    同理，当且仅当时， ＞0，

    综上，满足的所有正整数为1和2． 13分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆，过点作直线与椭圆交于两点．

    （1）若点平分线段，试求直线的方程；

    （2）设与满足（1）中条件的直线平行的直线与椭圆交于两点，与椭圆交于点，与椭圆交于点，求证：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】《选修4—4：坐标系与参数方程》

    已知直线l的参数方程为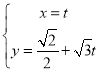 （t为参数），若以直角坐标系xOy的O点为极点，Ox方向为极轴，选择相同的长度单位建立极坐标系，得曲线C的极坐标方程为ρ＝2cos（θ－）．

    （1）求直线l的倾斜角和曲线的直角坐标方程；

    （2）若直线l与曲线C交于A，B两点，设点,求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】总体由编号为01，02，…，19，20的20个个体组成.利用下面的随机数表选取4个个体，选取方法从随机数表的第1行第4列数由左到右由上到下开始读取，则选出来的第4个个体的编号为（ ）

    第1行 78 16 65 71 02 30 60 14 01 02 40 60 90 28 01 98

    第2行 32 04 92 34 49 35 82 00 36 23 48 69 69 38 74 81

    A.10B.01C.09D.06

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，解关于的不等式；

    （2）若关于的不等式的解集是，求实数、的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l、m 、n 与平面α、β给出下列四个命题：

    ①若m∥l，n∥l，则m∥n； ②若m⊥α，m∥β，则α⊥β；

    ③若m∥α，n∥α，则m∥n；④若m⊥β，α⊥β，则m∥α

    其中，假命题的个数是（ ）

    A.1B.2C.3D.4

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥，底面为直角梯形，，底面，

    为的中点，为棱的中点.

    （Ⅰ）证明：平面；

    （Ⅱ）已知，求点到平面的距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    以直角坐标系的原点为极点，轴的非负半轴为极轴建立极坐标，且两坐标系取相同的长度单位．已知点的极坐标为，圆的极坐标方程为，若为曲线上的动点，且到定点的距离等于圆的半径．

    （1）求曲线的直角坐标方程；

    （2）若过点的直线的参数方程为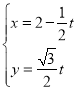（为参数），且直线与曲线交于、两点，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】四棱锥中，点在平面内的射影在棱上，，底面是梯形，，且．

    （1）求证：平面平面；

    （2）若直线与所成角为60°，求二面角的余弦值．

    查看答案和解析>>

    同步练习册答案