
【题目】已知函数![]() .
.
(1)讨论当![]() 时,函数
时,函数![]() 的单调性;
的单调性;
(2)当![]() 对任意的
对任意的![]() 恒成立,其中
恒成立,其中![]() .求
.求![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的导数![]() 满足f(x)+x
满足f(x)+x![]() >
>![]() 对x∈R恒成立,且实数x,y满足xf(x)﹣yf(y)>f(y)﹣f(x),则下列关系式恒成立的是( )
对x∈R恒成立,且实数x,y满足xf(x)﹣yf(y)>f(y)﹣f(x),则下列关系式恒成立的是( )
A.![]() B.ln(x2+1)>ln(y2+1)
B.ln(x2+1)>ln(y2+1)
C.![]() D.x﹣y>sinx﹣siny
D.x﹣y>sinx﹣siny
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对同一类的![]() ,
,![]() ,
,![]() ,
,![]() 四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
四项参赛作品,只评一项一等奖,在评奖揭晓前,甲、乙、丙、丁四位同学对这四项参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”;
作品获得一等奖”;
乙说:“![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“![]() ,
,![]() 两项作品未获得一等奖”;
两项作品未获得一等奖”;
丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
若这四位同学中只有两位说的话是对的,则获得一等奖的作品是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+2x+c,若不等式f(x)<0的解集是{x|-4<x<2}.
(1)求f(x)的解析式;
(2)判断f(x)在(0,+∞)上的单调性,并用定义证明;
(3)若函数f(x)在区间[m,m+2]上的最小值为-5,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】6名教师分配到3所薄弱学校去支教,每个学校至少分配一名教师,甲乙两人不能去同一所学校,丙丁两人必须去同一所学校,共有________种分配方案(用数字作答).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,短轴长是2.
,短轴长是2.
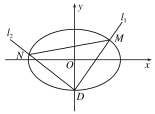
(1)求椭圆C的方程;
(2)设椭圆C的下顶点为D,过点D作两条互相垂直的直线l1,l2,这两条直线与椭圆C的另一个交点分别为M,N.设l1的斜率为k(k≠0),△DMN的面积为S,当![]() ,求k的取值范围.
,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科学研究表明:人类对声音有不的感觉,这与声音的强度![]() 单位:瓦
单位:瓦![]() 平方米
平方米![]() 有关
有关![]() 在实际测量时,常用
在实际测量时,常用![]() 单位:分贝
单位:分贝![]() 来表示声音强弱的等级,它与声音的强度I满足关系式:
来表示声音强弱的等级,它与声音的强度I满足关系式:![]() 是常数
是常数![]() ,其中
,其中![]() 瓦
瓦![]() 平方米
平方米![]() 如风吹落叶沙沙声的强度
如风吹落叶沙沙声的强度![]() 瓦
瓦![]() 平方米,它的强弱等级
平方米,它的强弱等级![]() 分贝.
分贝.
![]() 已知生活中几种声音的强度如表:
已知生活中几种声音的强度如表:
声音来源
声音大小 | 风吹落叶沙沙声 | 轻声耳语 | 很嘈杂的马路 |
强度 |
|
|
|
强弱等级 | 10 | m | 90 |
求a和m的值
![]() 为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.
为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com