
【题目】已知四棱锥P﹣ABCD中底面四边形ABCD是正方形,各侧面都是边长为2的正三角形,M是棱PC的中点.建立空间直角坐标系,利用空间向量方法解答以下问题: 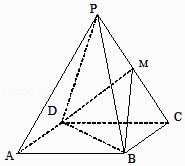
(1)求证:PA∥平面BMD;
(2)求二面角M﹣BD﹣C的平面角的大小.
【答案】
(1)证明:连结AC、BD交于点O,连结OP.
∵四边形ABCD是正方形,∴AC⊥BD∵PA=PC,∴OP⊥AC,
同理OP⊥BD,
以O为原点, ![]() 分别为x,y,z轴的正方向,建立空间直角坐标系O﹣xyz,
分别为x,y,z轴的正方向,建立空间直角坐标系O﹣xyz,
![]() ,
,
![]() ,
,
平面BMD的法向量为 ![]() ,
,
∵ ![]() ,
, ![]() ,又PA平面BMD,
,又PA平面BMD,
∴PA∥平面BMD
(2)解:平面ABCD的法向量为 ![]()
平面MBD的法向量为 ![]() ,
,
则 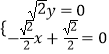 ,即
,即 ![]() ,
,
∴ ![]() …(9分)
…(9分)
二面角M﹣BD﹣C的平面角为α,
则 ![]() ,α=45°
,α=45°
∴二面角M﹣BD﹣C的平面角45°
【解析】(1)连结AC、BD交于点O,连结OP,以O为原点, ![]() 分别为x,y,z轴的正方向,建立空间直角坐标系O﹣xyz,利用向量法能证明PA∥平面BMD.(2)求出平面ABCD的法向量和平面MBD的法向量,利用向量法能求出二面角M﹣BD﹣C的平面角.
分别为x,y,z轴的正方向,建立空间直角坐标系O﹣xyz,利用向量法能证明PA∥平面BMD.(2)求出平面ABCD的法向量和平面MBD的法向量,利用向量法能求出二面角M﹣BD﹣C的平面角.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


科目:高中数学 来源: 题型:
【题目】关于函数 ![]() ,看下面四个结论( )
,看下面四个结论( )
①f(x)是奇函数;②当x>2007时, ![]() 恒成立;③f(x)的最大值是
恒成立;③f(x)的最大值是 ![]() ;④f(x)的最小值是
;④f(x)的最小值是 ![]() .其中正确结论的个数为:
.其中正确结论的个数为:
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在梯形ABCD中,AD∥BC,∠ABC=90°,点M、N分别在边AB、BC上,沿直线MD、DN、NM,分别将△AMD、△CDN、△BNM折起,点A,B,C重合于一点P. 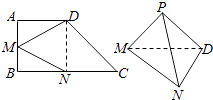
(1)证明:平面PMD⊥平面PND;
(2)若cos∠DNP= ![]() ,PD=5,求直线PD与平面DMN所成角的正弦值.
,PD=5,求直线PD与平面DMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知对任意实数x,有f(﹣x)=﹣f(x),g(﹣x)=g(x),且x>0时,f′(x)>0,g′(x)>0,则x<0时( )
A.f′(x)>0,g′(x)>0
B.f′(x)>0,g′(x)<0
C.f′(x)<0,g′(x)>0
D.f′(x)<0,g′(x)<0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的公差为2,前n项和为Sn , 且S1 , S2 , S4成等比数列. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=(﹣1)n﹣1 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,单位圆O与y轴负半轴交于点O',过点O'作与x轴平行的直线AB,射线O'P从O'A出发,绕着点O'逆时针方向旋转至O'B,在旋转的过程中,记∠AO'P=x(0<x<π),O'P所经过的在单位圆O内区域(阴影部分)的面积为S.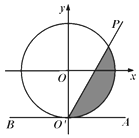
(1)如果 ![]() ,那么S=;
,那么S=;
(2)关于函数S=f(x)的以下两个结论:
①对任意 ![]() ,都有
,都有 ![]() ;
;
②对任意x1 , x2∈(0,π),且x1≠x2 , 都有 ![]() .
.
其中正确的结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设点O是平行四边形ABCD两条对角线的交点,给出下列向量组:
① ![]() 与
与 ![]() ;
;
② ![]() 与
与 ![]() ;
;
③ ![]() 与
与 ![]() ;
;
④ ![]() 与
与 ![]() .
.
其中可作为该平面其他向量基底的是( )
A.①②
B.①③
C.①④
D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( ) 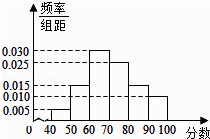
A.588
B.480
C.450
D.120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:方程 ![]() ﹣
﹣ ![]() =1表示焦点在y轴上的椭圆;命题q:双曲线
=1表示焦点在y轴上的椭圆;命题q:双曲线 ![]() ﹣
﹣ ![]() =1的离心率e∈(1,2).若命题p、q有且只有一个为真,求m的取值范围.
=1的离心率e∈(1,2).若命题p、q有且只有一个为真,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com