
已知函数y=f(x)是定义在区间[- ,
, ]上的偶函数,且
]上的偶函数,且
x∈[0, ]时,
]时,
(1)求函数f(x)的解析式;
(2)若矩形ABCD的顶点A,B在函数y=f(x)的图像上,顶点C,D在x轴上,求矩形ABCD面积的最大值.
(1)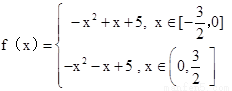 (2)6
(2)6
【解析】本题主要考查了分段函数、函数的最值及其几何意义及利用导数研究函数的极值,属于中档题.
(1)欲求函数f(x)的解析式,只须求出函数f(x)在x∈[-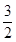 ,0]时的解析式即可,利用函数的偶函数性质即可由y轴右侧的表达式求出在y轴左侧的表达式.最后利用分段函数写出解析式即可.
,0]时的解析式即可,利用函数的偶函数性质即可由y轴右侧的表达式求出在y轴左侧的表达式.最后利用分段函数写出解析式即可.
(2)设A点在第一象限,坐标为A(t,-t2-t+5),利用对称性求出B点坐标,进而求出矩形ABCD面积,最后利用导数求出此面积表达式的最大值即可.
解(1)当x∈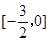 时,-x∈
时,-x∈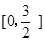 .
.
∴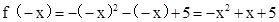 .又∵f(x)是偶函数,
.又∵f(x)是偶函数,
∴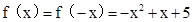 .
.
∴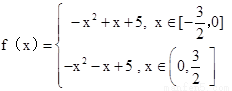 .
.
(2)由题意,不妨设A点在第一象限,
坐标为(t,-t2-t+5),其中t∈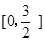
由图象对称性可知B点坐标为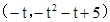 .
.
则S(t)= 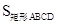 =
=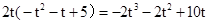
s′(t)=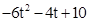 .由s′(t)=0,得
.由s′(t)=0,得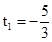 (舍去),
(舍去),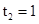 .
.
当0<t<1时,s′(t)>0;t>1时,s′(t)<0.
∴S(t)在(0,1]上单调递增,在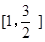 上单调递减.
上单调递减.
∴当t=1时,矩形ABCD的面积取得极大值6,
且此极大值也是S(t)在t∈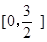 上的最大值.
上的最大值.
从而当t=1时,矩形ABCD的面积取得最大值6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2011 |
| 2 |
| 2011 |
| 3 |
| 2011 |
| 4 |
| 2011 |
| 2010 |
| 2011 |
| A、1005 | B、2010 |
| C、2011 | D、4020 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| lnx |
| x |
| 1 |
| e |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1-x | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com