Question

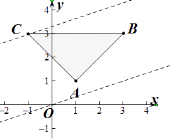
【题目】在直角坐标系xOy中，已知点A（1，1），B（3，3），点C在第二象限，且△ABC是以∠BAC为直角的等腰直角三角形．点P（x，y）在△ABC三边围城的区域内（含边界）．
（1）若 + + = 求| |；
（2）设 =m +n （m，n∈R），求m+2n的最大值．

Answer 1

【答案】
（1）解：设C（a，b），a＜0，b＞0，

∵A（1，1），B（3，3），

∴ =（2，2）， =（a﹣1，b﹣1），

∵△ABC是以∠BAC为直角的等腰直角三角形，

∴| |=| |， =0，

∴ ，

解得a=﹣1，b=3

∴C（﹣1，3），

设P（x，y），

∵ + + = ，

∴（1﹣x，1﹣y）+（3﹣x，3﹣y）+（﹣1﹣x，3﹣y）=（0，0），

∴3﹣3x=0，7﹣3y=0

∴x=1，y= ，

∴P（1， ），

∴| |= =

（2）解：∵ =（﹣2，2）， =m +n （m，n∈R），

∴（x，y）=m（2，2）+n（﹣2，2）=（2m﹣2n，2m+2n），

∴x=2m﹣2n，y=2m+2n，

∴m= （x+y），2n= （y﹣x），

∴m+2n=﹣ x+ y，

设z=3y﹣x，直线z=3y﹣x经过点C（﹣1，3）时，z取得最大值，

即m+2n= + ×3=

【解析】（1）设C（a，b），a＜0，b＞0，根据向量的坐标运算和向量的模，以及向量的垂直的条件求出点C的坐标，再根据向量的加减运算求出P的坐标，问题得以解决，（2）根据向量的坐标运算，以及线性规划，即可求出答案．
【考点精析】通过灵活运用平面向量的基本定理及其意义，掌握如果、是同一平面内的两个不共线向量，那么对于这一平面内的任意向量，有且只有一对实数、，使即可以解答此题．