
【题目】设![]() 为坐标原点,动点
为坐标原点,动点![]() 在圆
在圆![]() 上,过
上,过![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 满足
满足![]() .
.
(1)求点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)直线![]() 上的点
上的点![]() 满足
满足![]() .过点
.过点![]() 作直线
作直线![]() 垂直于线段
垂直于线段![]() 交
交![]() 于点
于点![]() .
.
(ⅰ)证明:![]() 恒过定点;
恒过定点;
(ⅱ)设线段![]() 交
交![]() 于点
于点![]() ,求四边形
,求四边形![]() 的面积.
的面积.
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】某便利店统计了今年第一季度各个品类的销售收入占比和净利润占比,并将部分品类的这两个数据制成如下统计图(注:销售收入占比![]() ,净利润占比
,净利润占比![]() ,净利润
,净利润![]() 销售收入
销售收入![]() 成本
成本![]() 各类费用),现给出下列判断:
各类费用),现给出下列判断:
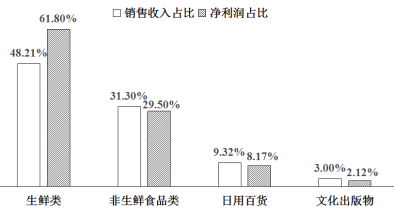
①该便利店第一季度至少有一种品类是亏损的;
②该便利店第一季度的销售收入中“生鲜类”贡献最大;
③该便利店第一季度“非生鲜食品类”的净利润一定高于“日用百货”的销售收入;
④该便利店第一季度“生鲜类”的销售收入比“非生鲜食品类”的销售收入多![]() .
.
则上述判断中正确的是( )
A.①②B.②③C.①④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
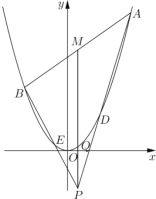
【题目】如图,已知点![]() 是
是![]() 轴下方(不含
轴下方(不含![]() 轴)一点,抛物线
轴)一点,抛物线![]() 上存在不同的两点
上存在不同的两点![]() 、
、![]() 满足
满足![]() ,
,![]() ,其中
,其中![]() 为常数,且
为常数,且![]() 、
、![]() 两点均在
两点均在![]() 上,弦
上,弦![]() 的中点为
的中点为![]() .
.
(1)若![]() 点坐标为
点坐标为![]() ,
,![]() 时,求弦
时,求弦![]() 所在的直线方程;
所在的直线方程;
(2)在(1)的条件下,如果过![]() 点的直线
点的直线![]() 与抛物线
与抛物线![]() 只有一个交点,过
只有一个交点,过![]() 点的直线
点的直线![]() 与抛物线
与抛物线![]() 也只有一个交点,求证:若
也只有一个交点,求证:若![]() 和
和![]() 的斜率都存在,则
的斜率都存在,则![]() 与
与![]() 的交点
的交点![]() 在直线
在直线![]() 上;
上;
(3)若直线![]() 交抛物线
交抛物线![]() 于点
于点![]() ,求证:线段
,求证:线段![]() 与
与![]() 的比为定值,并求出该定值.
的比为定值,并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
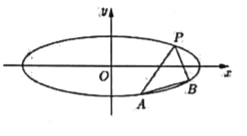
【题目】椭圆![]() 的焦距是
的焦距是![]() ,长轴长是短轴长3倍,任作斜率为
,长轴长是短轴长3倍,任作斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点(如图所示),且点
两点(如图所示),且点![]() 在直线
在直线![]() 的左上方.
的左上方.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() ,求
,求![]() 的面积;
的面积;
(3)证明:![]() 的内切圆的圆心在一条定直线上。
的内切圆的圆心在一条定直线上。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面直角坐标系![]() 中,曲线
中,曲线![]() 的方程为
的方程为![]() ,以原点
,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .若将曲线
.若将曲线![]() 上的所有点的横坐标缩小到原来的一半,纵坐标伸长到原来的
上的所有点的横坐标缩小到原来的一半,纵坐标伸长到原来的![]() 倍,得曲线
倍,得曲线![]() .
.
(1)写出直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() , 直线
, 直线![]() 与曲线
与曲线![]() 的两个交点分别为
的两个交点分别为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线C:
是抛物线C:![]() 上的一点,过P作互相垂直的直线PA,PB.与抛物线C的另一交点分别是A,B.
上的一点,过P作互相垂直的直线PA,PB.与抛物线C的另一交点分别是A,B.
(1)若直线AB的斜率为![]() ,求AB方程;
,求AB方程;
(2)设![]() ,当
,当![]() 时,求△PAB的面积.
时,求△PAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
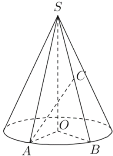
【题目】如图所示,圆锥的底面![]() 半径为2,
半径为2,![]() 是圆周上的定点,动点
是圆周上的定点,动点![]() 在圆周上逆时针旋转,设
在圆周上逆时针旋转,设![]() (
(![]() ),
),![]() 是母线
是母线![]() 的中点,已知当
的中点,已知当![]() 时,
时,![]() 与底面所成角为
与底面所成角为![]() .
.
(1)求该圆锥的侧面积;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上,![]() ,
,![]() ,且
,且![]() 的离心率为
的离心率为![]() ,抛物线
,抛物线![]() ,点
,点![]() 在
在![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作
作![]() 的切线
的切线![]() ,若
,若![]() ,直线
,直线![]() 与
与![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com