
如图,已知半径为 的⊙
的⊙ 与
与 轴交于
轴交于 、
、 两点,
两点, 为⊙
为⊙ 的切线,切点为
的切线,切点为 ,且
,且 在第一象限,圆心
在第一象限,圆心 的坐标为
的坐标为 ,二次函数
,二次函数 的图象经过
的图象经过 、
、 两点.
两点.

(1)求二次函数的解析式;
(2)求切线 的函数解析式;
的函数解析式;
(3)线段 上是否存在一点
上是否存在一点 ,使得以
,使得以 、
、 、
、 为顶点的三角形与
为顶点的三角形与 相似.若存在,请求出所有符合条件的点
相似.若存在,请求出所有符合条件的点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(1)二次函数的解析式为 ;(2)切线
;(2)切线 的函数解析式为
的函数解析式为 ;
;
(3)点 的坐标为
的坐标为 或
或 .
.
【解析】
试题分析:(1)先求出圆 的方程,并求出圆
的方程,并求出圆 与
与 轴的交点
轴的交点 和
和 的坐标,然后将点
的坐标,然后将点 和
和 的坐标代入二次函数
的坐标代入二次函数 中解出
中解出 和
和 的值,从而确定二次函数的解析式;(2)由于切线
的值,从而确定二次函数的解析式;(2)由于切线 过原点,可设切线
过原点,可设切线 的函数解析式为
的函数解析式为 ,利用直线
,利用直线 与圆
与圆 求出
求出 值,结合点
值,结合点 的位置确定切线
的位置确定切线 的函数解析式;(3)对
的函数解析式;(3)对 或
或 进行分类讨论,充分利用几何性质,从而确定点
进行分类讨论,充分利用几何性质,从而确定点 的坐标.
的坐标.
试题解析:(1)由题意知,圆 的方程为
的方程为 ,令
,令 ,解得
,解得 或
或 ,
,
故点 的坐标为
的坐标为 ,点
,点 的坐标为
的坐标为 ,
,
由于二次函数 经过
经过 、
、 两点,则有
两点,则有 ,解得
,解得 ,
,
故二次函数的解析式为 ;
;
(2)设直线 所对应的函数解析式为
所对应的函数解析式为 ,由于点
,由于点 在第一象限,则
在第一象限,则 ,
,
由于直线 与圆
与圆 相切,则
相切,则 ,解得
,解得 ,
,
故切线 的函数解析式为
的函数解析式为 ;
;
(3)由图形知,在 中,
中, ,
, ,
, ,
,
在 中,
中, ,由于
,由于 ,因为
,因为 ,
,
则必有 或
或 ,
,
联立 ,解得
,解得 ,故点
,故点 的坐标为
的坐标为 ,
,
当 时,直线
时,直线 的方程为
的方程为 ,联立
,联立 ,于是点
,于是点 的坐标为
的坐标为 ;
;
当 时,
时, ,由于点
,由于点 为线段
为线段 的中点,故点
的中点,故点 为线段
为线段 的中点,
的中点,
此时点 的坐标为
的坐标为 .
.
综上所述,当点 的坐标为
的坐标为 或
或 时,
时, .
.
考点:1.二次函数的解析式;2.直线与圆的位置关系;3.相似三角形


科目:高中数学 来源: 题型:

| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
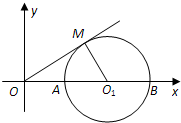 如图,已知半径为1的⊙O1与x轴交于A,B两点,OM为⊙O1的切线,切点为M,且M在第一象限,圆心O1的坐标为(2,0),二次函数y=-x2+bx+c的图象经过A,B两点.
如图,已知半径为1的⊙O1与x轴交于A,B两点,OM为⊙O1的切线,切点为M,且M在第一象限,圆心O1的坐标为(2,0),二次函数y=-x2+bx+c的图象经过A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:
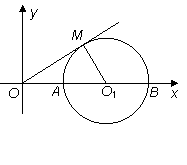
如图,已知半径为1的⊙O1与![]() 轴交于
轴交于![]() 两点,
两点,![]() 为⊙O1的切线,切点为
为⊙O1的切线,切点为![]() ,且
,且![]() 在第一象限,圆心
在第一象限,圆心![]() 的坐标为
的坐标为![]() ,二次函数
,二次函数![]() 的图象经过
的图象经过![]() 两点.
两点.
(1)求二次函数的解析式;
(2)求切线![]() 的函数解析式;
的函数解析式;
(3)线段![]() 上是否存在一点
上是否存在一点![]() ,使得以
,使得以![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.若存在,请求出所有符合条件的点
相似.若存在,请求出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2011年上海市普陀区高考数学二模试卷(文理合卷)(解析版) 题型:解答题
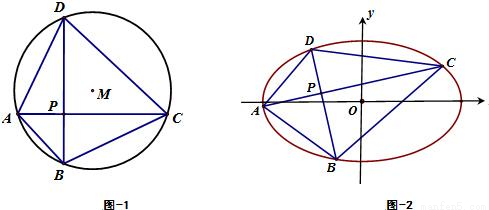
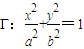 (a>b>0)的内接四边形ABCD的对角线AC和BD相互垂直且交于点P.试提出一个由类比获得的猜想,并尝试给予证明或反例否定.
(a>b>0)的内接四边形ABCD的对角线AC和BD相互垂直且交于点P.试提出一个由类比获得的猜想,并尝试给予证明或反例否定.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com