
如图,已知三棱柱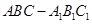 的侧棱与底面垂直,且
的侧棱与底面垂直,且 ,
,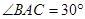 ,
,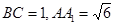 ,点
,点 分别为
分别为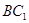 、
、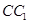 、
、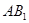 的中点.
的中点.
(1)求证: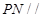 平面
平面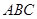 ;
;
(2)求证: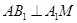 ;
;
(3)求二面角 的余弦值.
的余弦值.
解析试题分析:(1)线面平行的证明主要是走线面平行的判定定理这条路,因此必须在平面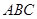 内寻找到一条与
内寻找到一条与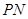 平行的直线,借助平几知识,这条直线不难找到;(2)在证明垂直关系时,如果几何证明有困难,也可从向量考虑;(3)求二面角的大小,主要是走向量这条路,它有固定步骤:首先求两个面的法向量,其次求法向量的余弦值进而得法向量的夹角,然后根据二面角是锐角还是钝角,决定其大小.
平行的直线,借助平几知识,这条直线不难找到;(2)在证明垂直关系时,如果几何证明有困难,也可从向量考虑;(3)求二面角的大小,主要是走向量这条路,它有固定步骤:首先求两个面的法向量,其次求法向量的余弦值进而得法向量的夹角,然后根据二面角是锐角还是钝角,决定其大小.
试题解析:(1)证明:连接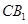 ,
,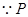 是
是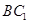 的中点 ,
的中点 ,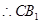 过点
过点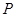 ,
,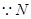 为
为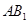 的中点,
的中点,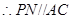 ,
,
又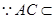 面
面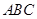 ,
,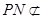 面
面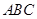 ,
,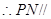 平面
平面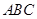 ;
;
(2)在直角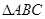 中,
中,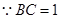 ,
,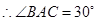 ,
,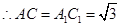 ,
,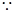 棱柱
棱柱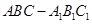 的侧棱与底面垂直,且
的侧棱与底面垂直,且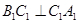 ,以点
,以点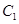 为原点,以
为原点,以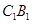 所在的直线为
所在的直线为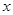 轴建立如图所示空间直角坐标系如图示,则
轴建立如图所示空间直角坐标系如图示,则 ,
,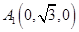 ,
,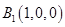 ,
,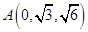 ,
,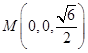 ,
,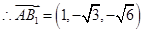 ,
,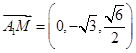 ,
,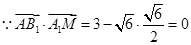 ,
, ;
;
(3)依题意得 ,
,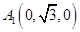 ,
, ,
,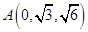 ,
,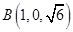 ,
,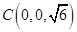 ,
,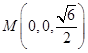 ,
,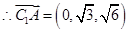 ,
,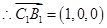
设面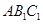 的一个法向量为
的一个法向量为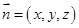 ,
,
由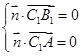 ,得
,得 ,令
,令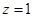 ,得
,得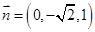 ,
,
同理可得面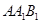 的一个法向量为
的一个法向量为 ,
,
故二面角的平面角 的余弦值为
的余弦值为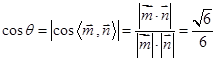 .
.
考点:空间向量与立体几何.


科目:高中数学 来源: 题型:解答题
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AB∥CD,AD⊥CD,且AB=AD=PD=1,CD=2,E为PC的中点.
(1)求证:BE∥平面PAD;
(2)求二面角E-BD-C的余弦值.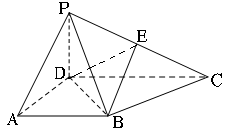
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在四棱锥E﹣ABCD中,矩形ABCD所在的平面与平面AEB垂直,且∠BAE=120°,AE=AB=4,AD=2,F,G,H分别为BE,AE,BC的中点
(1)求证:DE∥平面FGH;
(2)若点P在直线GF上,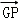 =λ
=λ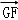 ,且二面角D﹣BP﹣A的大小为
,且二面角D﹣BP﹣A的大小为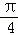 ,求λ的值.
,求λ的值.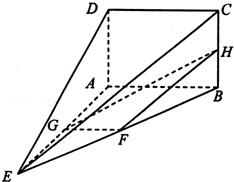
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知四棱锥P—GBCD中(如图),PG⊥平面GBCD,GD∥BC,GD=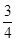 BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4
BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4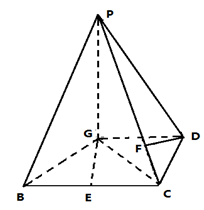
(1)求异面直线GE与PC所成角的余弦值;
(2)若F点是棱PC上一点,且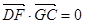 ,
,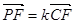 ,求
,求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com