
����Ŀ��Ϊ�˵�����Сѧ����ʹ�û�������������������������������Ϻ���������60����Сѧ�����ʾ�![]() �ݣ�
�ݣ� ![]() ��ѧ���μ����ʾ����飬�������������ݻ���������Ƶ�ʷֲ�ֱ��ͼ����ͼ��.
��ѧ���μ����ʾ����飬�������������ݻ���������Ƶ�ʷֲ�ֱ��ͼ����ͼ��.
��1��Ҫ����![]() ����Сѧ���÷ֲ�����ķ�����ȡ
����Сѧ���÷ֲ�����ķ�����ȡ![]() ����Сѧ����һ�����飬����
����Сѧ����һ�����飬����![]() ��Сʱ��ʱ�����Ӧ����������Ƕ��٣�
��Сʱ��ʱ�����Ӧ����������Ƕ��٣�
��2����ϣ��![]() ����Сѧ��ÿ��ʹ�û�����ʱ�䲻����
����Сѧ��ÿ��ʹ�û�����ʱ�䲻����![]() ��Сʱ���������
��Сʱ���������![]() ��ֵ����˵������.
��ֵ����˵������.

���𰸡���1��30����2��1.7
�������������������1���ֲ�����ķ������ø��ʼ��㣬��ֱ��ͼ��֪��ȡ��![]() ����Сѧ����ÿ��ʹ�û�������ʱ����
����Сѧ����ÿ��ʹ�û�������ʱ����![]() ��Сʱ��ʱ���ڵĸ���Ϊ
��Сʱ��ʱ���ڵĸ���Ϊ![]() ����10000����Сѧ�������Ϊ
����10000����Сѧ�������Ϊ![]() �ˣ���2��
�ˣ���2��![]() ����Сѧ��ÿ��ʹ�û�������ʱ�䲻����
����Сѧ��ÿ��ʹ�û�������ʱ�䲻����![]() ��Сʱ������
��Сʱ������![]() ������
������![]() �����
�����![]() .
.
���������
��1����ȡ��![]() ����Сѧ����ÿ��ʹ�û�������ʱ����
����Сѧ����ÿ��ʹ�û�������ʱ����![]() ��Сʱ��ʱ���ڵĸ���Ϊ
��Сʱ��ʱ���ڵĸ���Ϊ![]()
������![]() ����Сѧ��ÿ��ʹ�û�������ʱ����
����Сѧ��ÿ��ʹ�û�������ʱ����![]() ��Сʱ��ʱ���ڵ�����Ϊ
��Сʱ��ʱ���ڵ�����Ϊ![]() ��
��
��������![]() ������
������![]() ��Сʱ��ʱ�����Ӧ���������Ϊ
��Сʱ��ʱ�����Ӧ���������Ϊ![]() ��.
��.
��2����3���Ƶ��֮��Ϊ![]() ����
����![]() ��Ƶ����Ϊ
��Ƶ����Ϊ![]() ��ϣ��
��ϣ��![]() ����Сѧ��ÿ��ʹ�û�������ʱ�䲻����
����Сѧ��ÿ��ʹ�û�������ʱ�䲻����![]() ��Сʱ������
��Сʱ������![]() ������
������![]() �����
�����![]() .
.


 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
�У� ![]() ƽ��
ƽ��![]() �ֱ�Ϊ
�ֱ�Ϊ![]() ��
��![]() ���е㣬
���е㣬 ![]() �DZ߳�Ϊ
�DZ߳�Ϊ![]() ���������Σ�
���������� ![]() .
.
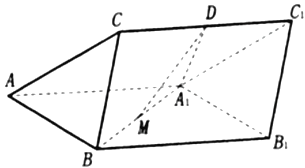
��1��֤���� ![]() ƽ��
ƽ��![]() ��
��
��2��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵ![]() �У�����Բ
�У�����Բ![]() �Ľ���Ϊ
�Ľ���Ϊ![]() �����ҽ���
�����ҽ���![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() �ཻ��
�ཻ��![]() ���㣬��
���㣬��![]() ���ܳ�Ϊ���᳤��
���ܳ�Ϊ���᳤��![]() ��.
��.
��������Բ![]() �������ʣ�
�������ʣ�
������![]() ��б��Ϊ
��б��Ϊ![]() ������Բ
������Բ![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹ��
��ʹ��![]() �������ڣ������
�������ڣ������![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ��ֱ��
��ֱ��![]() ��������ԭ�㣬������
��������ԭ�㣬������![]() ������������Ϊ
������������Ϊ![]() ����Բ
����Բ![]() �ཻ��
�ཻ��![]() ��
��![]() ���㣬ֱ��
���㣬ֱ��![]() ���߶�
���߶�![]() ���е㣬ͬʱ��Բ
���е㣬ͬʱ��Բ![]() �ϴ���һ�����ҽ������ֱ��
�ϴ���һ�����ҽ������ֱ��![]() �Գƣ�
�Գƣ�
��1����ֱ��![]() �ķ��̣�
�ķ��̣�
��2������Բ![]() �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѡ��4��4������ϵ���������
��ֱ������ϵ�У���ԭ��Ϊ���㣬 ![]() ��������Ϊ���Ὠ������ϵ��ֱ��
��������Ϊ���Ὠ������ϵ��ֱ��![]() �ļ����귽��Ϊ
�ļ����귽��Ϊ![]() ������
������![]() �IJ�������Ϊ
�IJ�������Ϊ![]() ����
���� ![]() ������.
������.
������ֱ��![]() ��ֱ�����귽�̺�����
��ֱ�����귽�̺�����![]() ����ͨ���̣�
����ͨ���̣�
��������![]() ��
��![]() ����
����![]() ���㣬�ҵ�
���㣬�ҵ�![]() ��
�� ![]() Ϊֱ��
Ϊֱ��![]() �ϵĶ��㣬��
�ϵĶ��㣬��![]() �ܳ�����Сֵ.
�ܳ�����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ������������
������������![]() ��
�� ![]() ������Բ
������Բ![]() ������
������![]() .
.
��1������Բ![]() �ı����̣�
�ı����̣�
��2��������Բ![]() ����
����![]() ��б��Ϊ1��ֱ��
��б��Ϊ1��ֱ��![]() ����Բ
����Բ![]() ����
����![]() ���㣬���߶�
���㣬���߶�![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y=x+ ![]() ���������ʣ��������t��0����ô�ú����ڣ�0��
���������ʣ��������t��0����ô�ú����ڣ�0�� ![]() ]���Ǽ���������[
]���Ǽ���������[ ![]() ��+�ޣ�������������
��+�ޣ�������������
��1����f��x��=x+ ![]() �������ڣ�0��a]�ϵ���СֵΪ4����a��ֵ��
�������ڣ�0��a]�ϵ���СֵΪ4����a��ֵ��
��2�����ڣ�1���еĺ���������A�ϵ�ֵ����[4��5]�������䳤������A��ע�����䳤��=������Ҷ˵㩁�������ϵ㣩��
��3������1���к����Ķ�������[2��+�ޣ��ⲻ��ʽf��a2��a����f��2a+4����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ������
������![]() ��
��
�������ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
����������![]() �������������
�������������![]() ��
�� ![]() ����֤��
����֤�� ![]() ��(����eΪ��Ȼ�����ĵ���)
��(����eΪ��Ȼ�����ĵ���)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ����
����![]() ������
������![]() ����������
����������
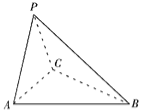
������֤����![]() ��
��
��������ƽ��![]() ��
��![]() ��
��![]() ��������
��������![]() �������
�������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com