
分析 (1)通过1与an作和、差可知1+an=$\frac{3{a}_{n-1}+3}{{a}_{n-1}+2}$、1-an=$\frac{1-{a}_{n-1}}{{a}_{n-1}+2}$,通过两式相除进而可知数列{$\frac{1-{a}_{n}}{1+{a}_{n}}$}是首项、公比均为$\frac{1}{3}$的等比数列;
(2)通过(1)可知$\frac{1-{a}_{n}}{1+{a}_{n}}$=$\frac{1}{{3}^{n}}$,进而可知bn=n(3n-1),利用错位相减法计算即得结论;
(3)通过(2)可知an=$\frac{{3}^{n}-1}{{3}^{n}+1}$,当n≥2时放缩可知$\frac{1}{{a}_{n}}$<1+$\frac{1}{{3}^{n-1}}$,相加计算即得结论.
解答 (1)证明:∵an=$\frac{2{a}_{n-1}+1}{{a}_{n-1}+2}$(n≥2,n∈N*),
∴1+an=1+$\frac{2{a}_{n-1}+1}{{a}_{n-1}+2}$=$\frac{3{a}_{n-1}+3}{{a}_{n-1}+2}$,
1-an=1-$\frac{2{a}_{n-1}+1}{{a}_{n-1}+2}$=$\frac{1-{a}_{n-1}}{{a}_{n-1}+2}$,
两式相除可知:$\frac{1-{a}_{n}}{1+{a}_{n}}$=$\frac{1}{3}$•$\frac{1-{a}_{n-1}}{1+{a}_{n-1}}$,
又∵$\frac{1-{a}_{1}}{1+{a}_{1}}$=$\frac{1-\frac{1}{2}}{1+\frac{1}{2}}$=$\frac{1}{3}$,
∴数列{$\frac{1-{a}_{n}}{1+{a}_{n}}$}是首项、公比均为$\frac{1}{3}$的等比数列;
(2)解:由(1)可知$\frac{1-{a}_{n}}{1+{a}_{n}}$=$\frac{1}{{3}^{n}}$,
整理得:an=$\frac{{3}^{n}-1}{{3}^{n}+1}$,
∴bn=n(3n+1)an=n(3n+1)$\frac{{3}^{n}-1}{{3}^{n}+1}$=n(3n-1),
记Tn=1•3+2•32+…+n•3n,3Tn=1•32+2•33+…+(n-1)•3n+n•3n+1,
错位相减得:-2Tn=3+32+33+…+3n-n•3n+1
=$\frac{3(1-{3}^{n})}{1-3}$-n•3n+1
=-$\frac{3}{2}$+$\frac{1-2n}{2}$•3n+1,
∴Tn=-$\frac{1}{2}$(-$\frac{3}{2}$+$\frac{1-2n}{2}$•3n+1)=$\frac{3}{4}$+$\frac{2n-1}{4}$•3n+1,
∴数列{bn}的前n项和Sn=Tn-$\frac{n(n+1)}{2}$=$\frac{3}{4}$+$\frac{2n-1}{4}$•3n+1-$\frac{n(n+1)}{2}$;
(3)证明:由(2)可知an=$\frac{{3}^{n}-1}{{3}^{n}+1}$,
则当n≥2时,$\frac{1}{{a}_{n}}$=$\frac{{3}^{n}+1}{{3}^{n}-1}$=1+$\frac{2}{{3}^{n}-1}$<1+$\frac{2}{3}$•$\frac{1}{{3}^{n-1}-1}$<…<1+$\frac{2}{{3}^{n-1}}$•$\frac{1}{3-1}$=1+$\frac{1}{{3}^{n-1}}$,
∴$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{3}}$+…+$\frac{1}{{a}_{n}}$≤n+$\frac{1-\frac{1}{{3}^{n}}}{1-\frac{1}{3}}$=n+$\frac{3}{2}$-$\frac{1}{2×{3}^{n-1}}$<n+3.
点评 本题考查数列的通项及前n项和,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.


 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:选择题
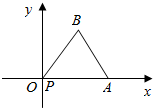 如图,某时刻点P与坐标原点O重合,将边长为2的等边三角形PAB沿x轴正方向滚动,设顶点P(x,y)的轨迹方程是y=f(x),对任意的t∈[1,2],函数g(x)=x3+x2[-$\frac{f(4)}{x}$+f(4)+$\frac{m}{2}$]在区间(t,3)上不是单调函数,则m的取值范围为( )
如图,某时刻点P与坐标原点O重合,将边长为2的等边三角形PAB沿x轴正方向滚动,设顶点P(x,y)的轨迹方程是y=f(x),对任意的t∈[1,2],函数g(x)=x3+x2[-$\frac{f(4)}{x}$+f(4)+$\frac{m}{2}$]在区间(t,3)上不是单调函数,则m的取值范围为( )| A. | (-$\frac{37}{3}$,-9) | B. | (-∞,-$\frac{37}{3}$) | C. | (-$\frac{37}{3}$,-5) | D. | (-9,-5) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x-y-1=0 | B. | x+y-1=0 | C. | $\sqrt{3}$x+y-$\sqrt{3}$=0 | D. | $\sqrt{3}$x-y+$\sqrt{3}$=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com