
对甲、乙两个班进行一门课程的考试,按照学生考试成绩优秀和不优秀统计后,得到下表:
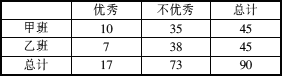
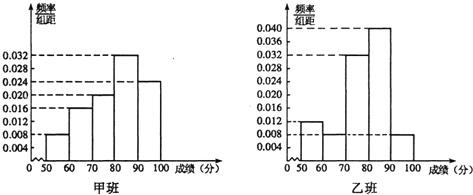
请画出列联表的二维条形图,通过图形判断成绩与班级是否有关,并利用独立性检验估计判断“成绩与班级有关”犯错误的概率.
科目:高中数学 来源: 题型:

| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | |||
| 成绩不优秀 | |||
| 总计 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| n(n11n22-n12n21)2 |
| n1+n2+n+1n+2 |

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | |||
| 成绩不优秀 | |||
| 总计 |
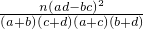 (此公式也可写成x2=
(此公式也可写成x2=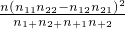 )
)
查看答案和解析>>
科目:高中数学 来源:2010-2011学年湖南省衡阳八中高三(下)第九次月考数学试卷(理科)(解析版) 题型:解答题

| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | |||
| 成绩不优秀 | |||
| 总计 |
 (此公式也可写成x2=
(此公式也可写成x2= )
)
查看答案和解析>>
科目:高中数学 来源:2011年福建省高三质量检查数学试卷(理科)(解析版) 题型:解答题

| 甲班(A方式) | 乙班(B方式) | 总计 | |
| 成绩优秀 | |||
| 成绩不优秀 | |||
| 总计 |
 (此公式也可写成x2=
(此公式也可写成x2= )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com