
【题目】如图,在多面体![]() 中,四边形
中,四边形![]() 是边长为
是边长为![]() 的菱形,
的菱形,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .
.
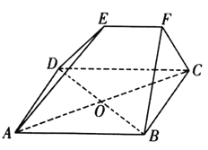
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 为等边三角形,点
为等边三角形,点![]() 为
为![]() 的中点,求二面角
的中点,求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】从2016年到2019年的某城市方便面销量情况如图所示:
年份 | 2016 | 2017 | 2018 | 2019 |
时间代号 | 1 | 2 | 3 | 4 |
年销量 | 462 | 444 | 404 | 385 |
(1)根据上表,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .用所求回归方程预测2020年(
.用所求回归方程预测2020年(![]() )方便面在该城市的年销量;
)方便面在该城市的年销量;
(2)某媒体记者随机对身边的10位朋友做了一次调查,其中3位受访者认为方便面是健康食品.现从这10人中抽取3人进行深度访谈,记![]() 表示随机抽取的3人认为方便面是健康食品的人数,求随机变量
表示随机抽取的3人认为方便面是健康食品的人数,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
参考公式:回归方程:![]() ,其中
,其中 ,
,![]() .
.
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】超市为了防止转基因产品影响民众的身体健康,要求产品在进入超市前必须进行两轮转基因检测,只有两轮都合格才能销售,否则不能销售.已知某产品第一轮检测不合格的概率为![]() ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为![]() ,两轮检测是否合格相互没有影响.
,两轮检测是否合格相互没有影响.
(1)求该产品不能销售的概率;
(2)如果产品可以销售,则每件产品可获利50元;如果产品不能销售,则每件产品亏损60元.已知一箱中有产品4件,记一箱产品获利![]() 元,求
元,求![]() 的分布列,并求出均值
的分布列,并求出均值![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)6个人按下列要求站一横排,甲、乙必须相邻,有多少种不同的站法?
(2)6个人按下列要求站一横排,甲不站左端,乙不站右端.有多少种不同的站法?
(3)用0,1,2,3,4,5这六个数字可以组成多少个六位数且是奇数(无重复数字的数)?
(4)用0,1,2,3,4,5这六个数字可以组成多少个个位上的数字不是5的六位数(无重复数字的数)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知过点![]() 的圆
的圆![]() 和直线
和直线![]() 相切,且圆心在直线
相切,且圆心在直线![]() 上.
上.
(1)求圆![]() 的标准方程;
的标准方程;
(2)点![]() ,圆
,圆![]() 上是否存在点
上是否存在点![]() ,使
,使![]()
![]() 若存在,求出点
若存在,求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com