
已知椭圆![]() 和圆
和圆![]()
![]() :,过椭圆上一点
:,过椭圆上一点![]() 引圆
引圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() .
.
(1)(ⅰ)若圆![]() 过椭圆的两个焦点,求椭圆的离心率
过椭圆的两个焦点,求椭圆的离心率![]() 的值;
的值;
(ⅱ)若椭圆上存在点![]() ,使得
,使得![]() ,求椭圆离心率
,求椭圆离心率![]() 的取值范围;
的取值范围;
(2)设直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() ,问当点P在椭圆上运动时,
,问当点P在椭圆上运动时,![]() 是否为定值?请证明你的结论.
是否为定值?请证明你的结论.

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源:2010年北京市崇文区高三年级二模理科试题 题型:解答题
(本小题共14分)
已知椭圆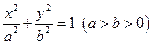 和圆
和圆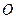 :
: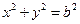 ,过椭圆上一点
,过椭圆上一点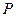 引圆
引圆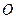 的两条切线,切点分别为
的两条切线,切点分别为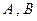 .
.
(Ⅰ)(ⅰ)若圆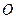 过椭圆的两个焦点,求椭圆的离心率
过椭圆的两个焦点,求椭圆的离心率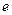
 ;
;
(ⅱ)若椭圆上存在点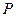 ,使得
,使得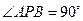 ,求椭圆离心率
,求椭圆离心率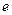 的取值范围;
的取值范围;
(Ⅱ)设直线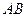 与
与 轴、
轴、 轴分别交于点
轴分别交于点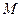 ,
,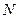 ,求证:
,求证: 为定值.
为定值.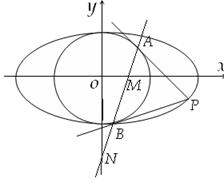
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省高三第四次(12月)阶段性测试数学试卷(解析版) 题型:解答题
已知椭圆 和圆
和圆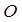 :
: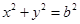 ,过椭圆上一点P引圆O的两条切线,切点分别为A,B.
,过椭圆上一点P引圆O的两条切线,切点分别为A,B.
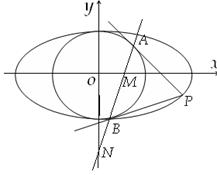
(1)(ⅰ)若圆O过椭圆的两个焦点,求椭圆的离心率e的值;
(ⅱ)若椭圆上存在点P,使得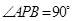 ,求椭圆离心率e的取值范围;
,求椭圆离心率e的取值范围;
(2)设直线AB与x轴、y轴分别交于点M,N,问当点P在椭圆上运动时, 是否为定值?请证明你的结论.
是否为定值?请证明你的结论.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省姜堰市高三第一学期学情调研数学试卷 题型:解答题
(本小题共16分)
已知椭圆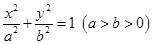 和圆
和圆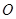 :
: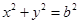 ,过椭圆上一点
,过椭圆上一点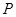 引圆
引圆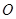 的两条切线,切点分别为
的两条切线,切点分别为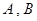 . (1)①若圆
. (1)①若圆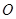 过椭圆的两个焦点,求椭圆的离心率
过椭圆的两个焦点,求椭圆的离心率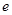 ; ②若椭圆上存在点
; ②若椭圆上存在点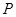 ,使得
,使得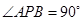 ,求椭圆离心率
,求椭圆离心率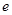 的取值(2)设直线
的取值(2)设直线 与
与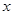 轴、
轴、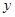 轴分别交于点
轴分别交于点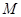 ,
,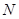 ,求证:
,求证: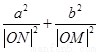 为定值.
为定值.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省姜堰市二中学高三学情调查数学试卷 题型:解答题
(本小题共16分)
已知椭圆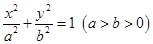 和圆
和圆 :
: ,过椭圆上一点
,过椭圆上一点 引圆
引圆 的两条切线,切点分别为
的两条切线,切点分别为 .
.
(1)①若圆 过椭圆的两个焦点,求椭圆的离心率
过椭圆的两个焦点,求椭圆的离心率 ; ②若椭圆上存在点
; ②若椭圆上存在点 ,使得
,使得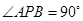 ,求椭圆离心率
,求椭圆离心率 的取值范围;
的取值范围;
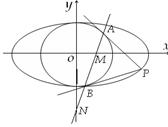
(2)设直线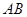 与
与 轴、
轴、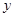 轴分别交于点
轴分别交于点 ,
, ,求证:
,求证: 为定值.
为定值.

查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省姜堰市高三第一学期学情调研数学试卷 题型:解答题
(本小题共16分)
已知椭圆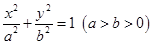 和圆
和圆 :
: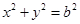 ,过椭圆上一点
,过椭圆上一点 引圆
引圆 的两条切线,切点分别为
的两条切线,切点分别为 . (1)①若圆
. (1)①若圆 过椭圆的两个焦点,求椭圆的离心率
过椭圆的两个焦点,求椭圆的离心率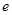 ; ②若椭圆上存在点
; ②若椭圆上存在点 ,使得
,使得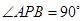 ,求椭圆离心率
,求椭圆离心率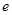 的取值(2)设直线
的取值(2)设直线 与
与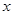 轴、
轴、 轴分别交于点
轴分别交于点 ,
, ,求证:
,求证: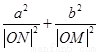 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com