
【题目】已知标有1~20号的小球20个,若我们的目的是估计总体号码的平均值,即20个小球号码的平均值.试验者从中抽取4个小球,以这4个小球号码的平均值估计总体号码的平均值,按下面方法抽样(按小号到大号排序):
(1)以编号2为起点,系统抽样抽取4个球,则这4个球的编号的平均值为____.
(2)以编号3为起点,系统抽样抽取4个球,则这4个球的编号的平均值为____.
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:
【题目】如图,设椭圆 ![]() (a>b>0)的左、右焦点分别为F1 , F2 , 点D在椭圆上.DF1⊥F1F2 ,
(a>b>0)的左、右焦点分别为F1 , F2 , 点D在椭圆上.DF1⊥F1F2 , ![]() =2
=2 ![]() ,△DF1F2的面积为
,△DF1F2的面积为 ![]() .
. 
(1)求椭圆的标准方程;
(2)设圆心在y轴上的圆与椭圆在x轴的上方有两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点,求圆的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
性别 是否需要志愿者 | 男 | 女 |
需要 | 40 | 30 |
不需要 | 160 | 270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
附:![]() ,其中
,其中![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,锐角![]() 和钝角
和钝角![]() 的终边分别与单位圆交于
的终边分别与单位圆交于![]() 两点.
两点.
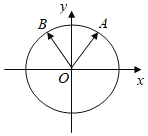
(Ⅰ)如果点![]() 纵坐标分别为
纵坐标分别为![]() ,求
,求![]() ;
;
(Ⅱ)若![]() 为
为![]() 轴上异于
轴上异于![]() 的点,且
的点,且![]() ,求点
,求点![]() 横坐标的取值范围.
横坐标的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2022年北京冬奥会,推广滑雪运动,某滑雪场开展滑雪促销活动.该滑雪场的收费标准是:滑雪时间不超过1小时免费,超过1小时的部分每小时收费标准为40元(不足1小时的部分按1小时计算).有甲、乙两人相互独立地来该滑雪场运动,设甲、乙不超过1小时离开的概率分别为![]() ,
,![]() ;1小时以上且不超过2小时离开的概率分别为
;1小时以上且不超过2小时离开的概率分别为![]() ,
,![]() ;两人滑雪时间都不会超过3小时.
;两人滑雪时间都不会超过3小时.
(1)求甲、乙两人所付滑雪费用相同的概率;
(2)设甲、乙两人所付的滑雪费用之和为随机变量ξ,求ξ的分布列与数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a∈R,f(x)= ![]() 为奇函数.
为奇函数.
(1)求函数F(x)=f(x)+2x﹣ ![]() ﹣1的零点;
﹣1的零点;
(2)设g(x)=2log2( ![]() ),若不等式f﹣1(x)≤g(x)在区间[
),若不等式f﹣1(x)≤g(x)在区间[ ![]() ,
, ![]() ]上恒成立,求实数k的取值范围.
]上恒成立,求实数k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】求满足下列条件的直线的方程:
(1)直线![]() 经过点
经过点![]() ,并且它的倾斜角等于直线
,并且它的倾斜角等于直线![]() 的倾斜角的2倍,求直线
的倾斜角的2倍,求直线![]() 的方程;
的方程;
(2)直线![]() 过点
过点![]() ,并且在
,并且在![]() 轴上的截距是
轴上的截距是![]() 轴上截距的
轴上截距的![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx-![]() )+1(A>0, ω>0)与ω=cosωx的部分图象如图所示。
)+1(A>0, ω>0)与ω=cosωx的部分图象如图所示。

(1)求A,a,b的值及函数f(x)的递增区间;
(2)若函数y= g(x-m)(m>![]() )与y= f(x)+ f(x-
)与y= f(x)+ f(x-![]() )的图象的对称轴完全相同,求m的最小值.
)的图象的对称轴完全相同,求m的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com