
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 上的点均在曲线
上的点均在曲线![]() 外,且对
外,且对![]() 上任意一点
上任意一点![]() ,
,![]() 到直线
到直线![]() 的距离等于该点与曲线
的距离等于该点与曲线![]() 上点的距离的最小值.
上点的距离的最小值.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若点![]() 是曲线
是曲线![]() 的焦点,过
的焦点,过![]() 的两条直线
的两条直线![]() 关于
关于![]() 轴对称,且分别交曲线
轴对称,且分别交曲线![]() 于
于![]() ,若四边形
,若四边形![]() 的面积等于
的面积等于![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)求得![]() 的圆心和半径,利用题目所给“
的圆心和半径,利用题目所给“![]() 到直线
到直线![]() 的距离等于该点与曲线
的距离等于该点与曲线![]() 上点的距离的最小值”列方程,化简这个方程可求得轨迹
上点的距离的最小值”列方程,化简这个方程可求得轨迹![]() 的方程.(2)设出直线
的方程.(2)设出直线![]() 的方程,代入抛物线的方程求得弦长
的方程,代入抛物线的方程求得弦长![]() 的值.根据对称性求得
的值.根据对称性求得![]() 的值,利用面积公式列方程,从而求得所求直线的斜率,进而求得直线方程.
的值,利用面积公式列方程,从而求得所求直线的斜率,进而求得直线方程.
(1)由已知得曲线![]() 是以
是以![]() 为圆心,
为圆心,![]() 为半径的圆.设
为半径的圆.设![]() ,则
,则![]() 到直线
到直线![]() 的距离等于
的距离等于![]() ,又
,又![]() 到圆
到圆![]() 上的点的距离的最小值为
上的点的距离的最小值为![]() ,所以由已知可得
,所以由已知可得![]() ,化简得
,化简得![]() , 所以曲线
, 所以曲线![]() 的方程为
的方程为![]() .(2)依题意可知,直线
.(2)依题意可知,直线![]() 的斜率存在,并且互为相反数.设直线
的斜率存在,并且互为相反数.设直线![]() 的方程
的方程![]() ,代入抛物线方程并化简得
,代入抛物线方程并化简得![]() ,故
,故![]() ,由弦长公式得
,由弦长公式得![]() ,同理
,同理![]() .下面求直线
.下面求直线![]() 夹角的正弦值.设直线
夹角的正弦值.设直线![]() 的倾斜角为
的倾斜角为![]() ,则
,则![]() ,则直线
,则直线![]() 夹角为
夹角为![]() ,且
,且![]() .所以四边形
.所以四边形![]() 的面积为
的面积为![]() ,
,![]() ,解得
,解得![]() ,此时直线
,此时直线![]() 的斜率为
的斜率为![]() ,根据对称性可知.当直线
,根据对称性可知.当直线![]() 斜率为
斜率为![]() 时,
时,![]() 斜率为
斜率为![]() ,也符合题意.故
,也符合题意.故![]() ,所求的直线方程为
,所求的直线方程为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,![]() 底面ABC,
底面ABC,![]() .点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,
.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,![]() ,
,![]() .
.
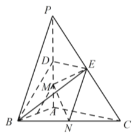
(1)求证:![]() 平面BDE;
平面BDE;
(2)求二面角C-EM-N的正弦值.
(3)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为![]() ,求线段AH的长.
,求线段AH的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网站针对“2016年春节放假安排”开展网上问卷调查,提出了A,B两种放假方案,调查结果如表:(单位:万人)
人群 | 青少年 | 中年人 | 老年人 |
支持A方案 | 200 | 400 | 800 |
支持B方案 | 100 | 100 | n |
已知从所有参与调查的人中任选1人是“老年人”的概率为![]() .
.
(1)求n的值;
(2)从参与调查的“老年人”中,用分层抽样的方法抽取6人,在这6人中任意选取2人,求恰好有1人“支持B方案”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从4名书法比赛一等奖的同学和2名绘画比赛一等奖的同学中选出2名志愿者,参加某项服务工作.
(1)求选出的两名志愿者都是获得书法比赛一等奖的同学的概率;
(2)求选出的两名志愿者中一名是获得书法比赛一等奖,另一名是获得绘画比赛一等奖的同学的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知梯形![]() 如图(1)所示,其中
如图(1)所示,其中![]() ,
, ![]() ,四边形
,四边形![]() 是边长为
是边长为![]() 的正方形,现沿
的正方形,现沿![]() 进行折叠,使得平面
进行折叠,使得平面![]() 平面
平面![]() ,得到如图(2)所示的几何体.
,得到如图(2)所示的几何体.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)已知点![]() 在线段
在线段![]() 上,且
上,且![]() 平面
平面![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校一位教师要去某地参加全国数学优质课比赛,已知他乘火车、轮船、汽车、飞机直接去的概率分别为0.3、0.1、0.2、0.4.
(1)求他乘火车或乘飞机去的概率;
(2)他不乘轮船去的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数据![]() 是郑州市普通职工
是郑州市普通职工![]() 个人的年收入,若这
个人的年收入,若这![]() 个数据的中位数为
个数据的中位数为![]() ,平均数为
,平均数为![]() ,方差为
,方差为![]() ,如果再加上世界首富的年收入
,如果再加上世界首富的年收入![]() ,则这
,则这![]() 个数据中,下列说法正确的是( )
个数据中,下列说法正确的是( )
A.年收入平均数大大增大,中位数一定变大,方差可能不变
B.年收入平均数大大增大,中位数可能不变,方差变大
C.年收入平均数大大增大,中位数可能不变,方差也不变
D.年收入平均数可能不变,中位数可能不变,方差可能不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某投资公司计划在甲、乙两个互联网创新项目上共投资1200万元,每个项目至少要投资300万元.根据市场分析预测:甲项目的收益![]() 与投入
与投入![]() 满足
满足![]() ,乙项目的收益
,乙项目的收益![]() 与投入
与投入![]() 满足
满足![]() .设甲项目的投入为
.设甲项目的投入为![]() .
.
(1)求两个项目的总收益关于![]() 的函数
的函数![]() .
.
(2)如何安排甲、乙两个项目的投资,才能使总收益最大?最大总收益为多少?(注:收益与投入的单位都为“万元”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com