D
分析:根据题意,首先计算由1、2、3、4、5、6组成的没有重复数字的六位偶数个数,具体是:先取1个偶数字数放在个位,再将其他5个数安排在前五个位置,由分步计数原理可得其个数,进而分析“吉祥数”的个数,分5在首位、在十位、在其他位置,3种情况讨论,由分类计数原理计算可得其情况数目,进而由等可能事件的概率,计算可得答案.
解答:根据题意,用1、2、3、4、5、6组成没有重复数字的六位偶数,
1、2、3、4、5、6中有3个偶数,则个位数字有3种情况,把其他5个数安排在前五个位置,有A
55种情况,
则得到的六位偶数共有3A
55=360个,
5只与偶数数字相邻,即5左右两边都是偶数,分种情况讨论:
若5在首位,在2、4、6中任选2个,一个放在第二位,一个放在个位,则有A
32×A
33种情况,
若5在十位,则需在2、4、6中任选2个,一个放在个位,一个放在百位,则有A
32×A
33种情况,
若5在其他位置,则需在2、4、6中任选1个放在个位,将剩余的2个放在5的两边,与剩余的2个奇数进行全排列,
则有C
31×A
22×A
33种情况,
吉祥数的个数有A
32×A
33+A
32×A
33+C
31×A
22×A
33=36+36+36=108个,
则出现“吉祥数”的概率P=
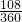
=

;
故选D.
点评:本题考查等可能事件的概率,涉及排列组合的应用,难点在于对吉祥数的情况进行分类讨论,容易遗漏5在十位的情况.





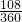 =
= ;
;

 阅读快车系列答案
阅读快车系列答案